题目内容
设数列{an}满足:a1=2,an+1=an+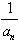 (n=1,2,3,…)。
(n=1,2,3,…)。
(1)证明: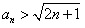 对一切n恒成立;
对一切n恒成立;
(2)令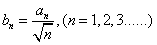 ,判断bn与bn+1的大小,并说明理由。
,判断bn与bn+1的大小,并说明理由。
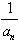 (n=1,2,3,…)。
(n=1,2,3,…)。(1)证明:
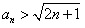 对一切n恒成立;
对一切n恒成立;(2)令
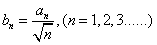 ,判断bn与bn+1的大小,并说明理由。
,判断bn与bn+1的大小,并说明理由。解:(1)当n=1时,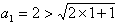 ,不等式成立
,不等式成立
假设n=k成立,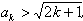 成立
成立
当n=k+1时,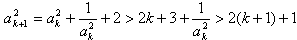
∴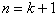 时,
时,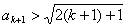 时成立
时成立
综上由数学归纳法可知,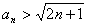 对一切正整数成立。
对一切正整数成立。
(2)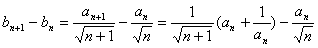
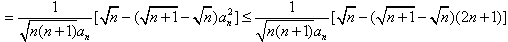
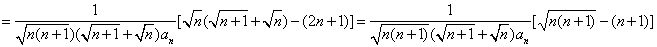
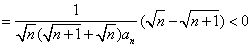
所以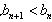 。
。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目