题目内容
下列说法:
①“ ,使
,使 ”的否定是“
”的否定是“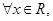 使
使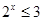 ”;
”;
②函数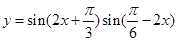 的最小正周期是
的最小正周期是 ;
;
③命题“函数f(x)在x=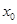 处有极值,则
处有极值,则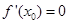 ”的否命题是真命题;
”的否命题是真命题;
④f(x)是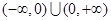 上的奇函数,x>0时的解析式是
上的奇函数,x>0时的解析式是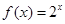 ,则x<0时的解析式为
,则x<0时的解析式为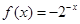 .
.
其中正确的说法是 .
①④
解析试题分析:①“?x∈R,使2x>3”的否定是“?x∈R,使2x≤3”,特称命题的否定是全称命题,由书写规则知此命题是正确命题;②函数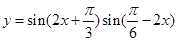 的最小正周期是π,由于
的最小正周期是π,由于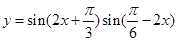 =
= ,由公式求得其周期是
,由公式求得其周期是 ,故此命题不正确;③命题“函数f(x)在x=x处有极值,则
,故此命题不正确;③命题“函数f(x)在x=x处有极值,则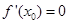 ”的否命题是真命题,由于
”的否命题是真命题,由于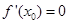 时,数f(x)在x=x处不一定有极值,故此命题不正确;④f(x)是(-∞,0)∪(0+∞)上的奇函数x>0的解析式是
时,数f(x)在x=x处不一定有极值,故此命题不正确;④f(x)是(-∞,0)∪(0+∞)上的奇函数x>0的解析式是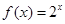 ,则x<0的解析式为
,则x<0的解析式为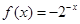 ,当x<0,-x>0,可得
,当x<0,-x>0,可得 ,故此命题正确.综上得,①④是正确命题.
,故此命题正确.综上得,①④是正确命题.
考点:1.命题的否定;2.函数奇偶性的性质;3.三角函数的周期性及其求法.

练习册系列答案
相关题目
”a<0”是”函数 在区间
在区间 上单调递增”的( )
上单调递增”的( )
| A.必要不充分条件 | B.充要条件 |
| C.既不充分也不必要条件 | D.充分不必要条件 |
 的值是( ).
的值是( ).
A. | B. | C. | D. |
已知函数 在
在 上是减函数,则
上是减函数,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
函数 ,若函数
,若函数 在区间(
在区间( ,
, +1)上单调递增,则实数
+1)上单调递增,则实数
的取值范围是( )
A.(-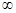 ,1 ,1 | B.[1, 4] |
C. 4, + 4, +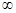 ) ) | D.(-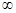 ,1 ,1 ∪[4, + ∪[4, +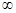 ) ) |
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
 ,则
,则 .
. ,则
,则
 的定义域为 .
的定义域为 .