题目内容
已知幂函数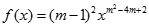 在
在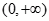 上单调递增,函数
上单调递增,函数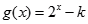 .
.
(1)求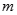 的值;
的值;
(2)当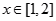 时,记
时,记 ,
,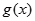 的值域分别为集合
的值域分别为集合 ,若
,若 ,求实数
,求实数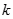 的取值范围.
的取值范围.
(1)m=0;(2)[0,1].
解析试题分析:(1)根据幂函数的定义个性质即可求出.
(2)根据幂函数和指数函数的单调性,分别求出其值域,再根据A∪B=A,得到关于k的不等式组,解得即可.
试题解析:解:(1)依题意得: ,解得m=0或m=2
,解得m=0或m=2
当m=2时, 在(0,+∞)上单调递减,与题设矛盾,舍去
在(0,+∞)上单调递减,与题设矛盾,舍去
∴m=0.
(2)由(1)可知 ,
,
当x∈[1,2]时,f(x),g(x)单调递增,
∴A=[1,4],B=[2-k,4-k],
∵A∪B=A,
∴ ,
,
∴
 0≤k≤1.
0≤k≤1.
故实数k的取值范围是[0,1].
考点:幂函数的性质.

练习册系列答案
相关题目
设 ,若函数
,若函数 为单调递增函数,且对任意实数
为单调递增函数,且对任意实数 ,都有
,都有 (
( 是自然对数的底数),则
是自然对数的底数),则 ( )
( )
| A.1 | B. | C.3 | D. |
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
某正弦型函数的图像如图,则该函数的解析式可以为( ). 
A. | B. |
C. | D. |
 的定义域为 .
的定义域为 . 是定义在
是定义在 上的偶函数,当
上的偶函数,当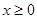 时,
时,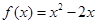
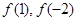 的值;
的值; 的解析式;并画出简图;
的解析式;并画出简图; 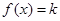 的根的情况。(只需写出结果,不要解答过程).
的根的情况。(只需写出结果,不要解答过程).
 .
. ,函数
,函数 在
在 上单调递减.则
上单调递减.则 的取值范围是 .
的取值范围是 .