题目内容
7.已知函数$f(x)=\frac{{cos(x-\frac{3π}{2})•sin(\frac{5π}{2}+x)}}{cos(-x-π)}$,g(x)=$\sqrt{2}sin(2x-\frac{π}{4})$(1)化简f(x);
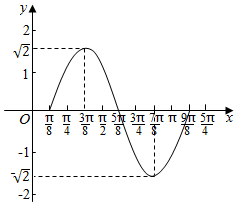
(2)利用“五点法”,按照列表-描点-连线三步,画出函数g(x)一个周期的图象;
(3)函数g(x)的图象可以由函数f(x)的图象经过怎样的变换得到?
分析 (1)由条件利用三角恒等变换,化简函数的解析式.
(2)用五点法作函数y=Asin(ωx+φ)在一个周期上的简图.
(3)由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:(1)$f(x)=\frac{(-sinx)•cosx}{-cosx}=sinx$.
(2)列表:
| 2x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | $\frac{9π}{8}$ |
| g(x) | 0 | $\sqrt{2}$ | 0 | -$\sqrt{2}$ | 0 |
(3)把f(x)=sinx的图象向右平移$\frac{π}{4}$个单位,可得y=sin(x-$\frac{π}{4}$)的图象;
再把横坐标变为原来的$\frac{1}{2}$倍,可得y=sin(2x-$\frac{π}{4}$)的图象;
最后把纵坐标变为原来的$\sqrt{2}$倍,可得y=$\sqrt{2}$sin(2x-$\frac{π}{4}$)的图象.
点评 本题主要考查三角恒等变换,用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为( )
如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为( )
 如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为( )
如图是某学校一名篮球运动员在10场比赛中所得分数的茎叶图,则该运动员在这10场比赛中得分的中位数为( )| A. | 15 | B. | 15.5 | C. | 16 | D. | 16.5 |
2.三棱柱ABC-A1B1C1中,侧棱AA1丄底面A1B1C1,底面三角形是正三角形,E是BC中点,则下列叙述正确的是( )
| A. | CC1与B1E是异面直线 | B. | AC丄平面ABB1A1 | ||
| C. | AE 丄 B1C1 | D. | A1C1∥平面AB1E |
 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为$(\frac{{\sqrt{5}-1}}{2},1)$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,延长B1F2与A2B2交于P点,若∠B1PA2为钝角,则此椭圆的离心率的取值范围为$(\frac{{\sqrt{5}-1}}{2},1)$.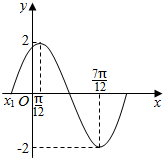 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)在一个周期内的图象如图所示.