题目内容
已知数列 ,
,  满足条件:
满足条件:
 ,
,  .
.
(1)求证数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ,并求使得
,并求使得 对任意
对任意 N*都成立的正整数
N*都成立的正整数 的最小值.
的最小值.
(1)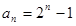 (2)正整数
(2)正整数 的最小值是5
的最小值是5
解析试题分析:(1)由数列的递推公式求数列的通项公式,根据等比数列的定义,只要证明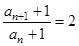 即可
即可
(2)由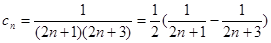 ,利用裂项相消法,可得
,利用裂项相消法,可得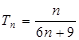 ,
,
然后证明数列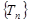 是一个递增数列,当
是一个递增数列,当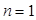 时,
时, 取得最小值
取得最小值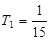 ,要使得
,要使得 对任意
对任意 N*都成立,结合(1)的结果,只需
N*都成立,结合(1)的结果,只需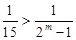 ,解之即可
,解之即可
(1)∵
∴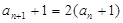 ,∵
,∵ ,
,
∴数列 是首项为2,公比为2的等比数列 .
是首项为2,公比为2的等比数列 .
∴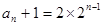 ∴
∴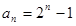
(2)∵ ,
,
∴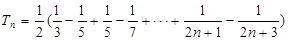
 .
.
∵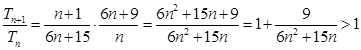 ,又
,又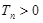 ,
,
∴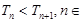 N*,即数列
N*,即数列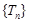 是递增数列.
是递增数列.
∴当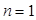 时,
时, 取得最小值
取得最小值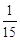 .
.
要使得 对任意
对任意 N*都成立,结合(1)的结果,只需
N*都成立,结合(1)的结果,只需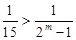 ,由此得
,由此得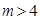 .∴正整数
.∴正整数 的最小值是5.
的最小值是5.
考点:等比数列,裂项相消法,递增数列的证明

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知函数 对应关系如表1所示,数列
对应关系如表1所示,数列 满足
满足 ,
, ,则
,则 .
.
 | 1 | 2 | 3 |
 | 3 | 2 | 1 |
 ,n∈N*,向量
,n∈N*,向量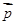 与
与 垂直,且a1=1.
垂直,且a1=1. 的前
的前 项和为
项和为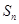 ,数列
,数列 是公比为
是公比为 的等比数列,
的等比数列, 是
是 和
和 的等比中项.
的等比中项. 的前
的前 .
. 的左、右顶点分别是
的左、右顶点分别是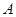 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 .若
.若 ,
, ,
, 成等比数列,求此椭圆的离心率.
成等比数列,求此椭圆的离心率.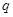 和
和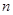 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合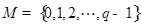 ,集合
,集合 .
.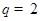 ,
,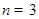 时,用列举法表示集合
时,用列举法表示集合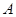 ;
;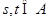 ,
,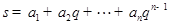 ,
,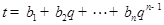 ,其中
,其中 证明:若
证明:若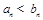 ,则
,则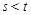 .
. 中,
中, ,前
,前 项的和是
项的和是 ,且
,且 ,
, .
.
 .
.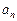 }的前n项和为
}的前n项和为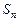 ,且
,且 .
.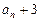 }为等比数列
}为等比数列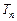
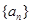 的前
的前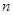 项和为
项和为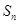 ,且
,且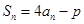 ,其中
,其中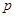 是不为零的常数.
是不为零的常数.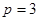 时,数列
时,数列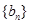 满足
满足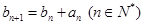 ,
,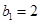 ,求数列
,求数列