题目内容
6.函数f(x)=cos4x•cos2x•cosx•sinx的最大值和最小正周期依次为 ( )| A. | $\frac{1}{8};\frac{π}{4}$ | B. | $\frac{1}{4};\frac{π}{2}$ | C. | $\frac{1}{2};π$ | D. | 1;2π |
分析 利用二倍角化简函数f(x),根据正弦函数的图象与性质求出f(x)的最大值与最小正周期.
解答 解:函数f(x)=cos4x•cos2x•cosx•sinx
=$\frac{1}{2}$cos4x•cos2x•sin2x
=$\frac{1}{4}$cos4x•sin4x
=$\frac{1}{8}$sin8x,
根据正弦函数的图象与性质,得
f(x)的最大值是$\frac{1}{8}$,
最小正周期为T=$\frac{2π}{ω}$=$\frac{2π}{8}$=$\frac{π}{4}$.
故选:A.
点评 本题考查了二倍角公式与正弦函数的图象和性质的应用问题,是基础题.

练习册系列答案
相关题目
14.已知动点P(x,y)满足$\sqrt{{x}^{2}+(y+3)^{2}}$+$\sqrt{{x}^{2}+(y-3)^{2}}$=6,则动点P的轨迹是( )
| A. | 双曲线 | B. | 线段 | C. | 抛物线 | D. | 椭圆 |
1.在△ABC中,a,b,c分别为∠A、∠B、∠C、的对边,若a+c=2b,且$sinB=\frac{4}{5}$,当△ABC的面积为$\frac{3}{2}$时,则b=( )
| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | 2 | C. | 4 | D. | 2+$\sqrt{3}$ |
16.已知倾斜角为α的直线l与直线x+2y-4=0垂直,则$cos(\frac{2017}{2}π-2α)$的值为( )
| A. | 2 | B. | $-\frac{1}{2}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
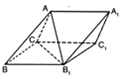 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AC=AB1.