题目内容
已知经过同一点的 N
N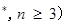 个平面,任意三个平面不经过同一条直线.若这
个平面,任意三个平面不经过同一条直线.若这 个平面将空间分成
个平面将空间分成 个部分,则
个部分,则 ,
, .
.
 N
N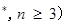 个平面,任意三个平面不经过同一条直线.若这
个平面,任意三个平面不经过同一条直线.若这 个平面将空间分成
个平面将空间分成 个部分,则
个部分,则 ,
, .
. 8, 

试题分析:
 的值即3个平面将空间分成几部分,取3个两两垂直的平面,满足题干要求,此时将空间分成8部分,
的值即3个平面将空间分成几部分,取3个两两垂直的平面,满足题干要求,此时将空间分成8部分, ;当
;当 时,每增加一个面,这个面就要与前面
时,每增加一个面,这个面就要与前面 个面都相交,因为过同一点,两平面如果有一个公共点就有一条公共直线,这样就会把前面平面划分的空间一分为二,即
个面都相交,因为过同一点,两平面如果有一个公共点就有一条公共直线,这样就会把前面平面划分的空间一分为二,即 ,累加得
,累加得
点评:本题的关键点在所有的平面都过同一点,这样新增加的平面与之前的所有平面都相交,将原来平面划分的空间一分为二,本题难度较大,学生不易找到入手点

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
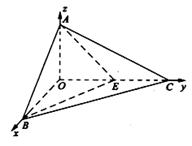
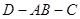 ,如图二,在二面角
,如图二,在二面角
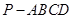 中,四边形
中,四边形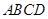 是菱形,
是菱形,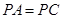 ,
,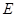 为
为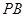 的中点.
的中点.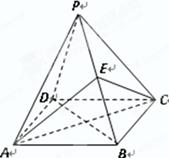
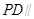 面
面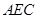 ; (2)求证:平面
; (2)求证:平面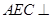 平面
平面 .
.
 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点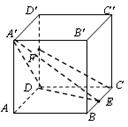
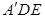
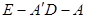 的平面角的余弦值.
的平面角的余弦值.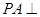 ⊙
⊙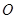 所在的平面,AB是⊙
所在的平面,AB是⊙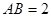 ,
,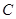 是⊙
是⊙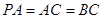 ,
,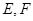 分别为
分别为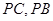 中点。
中点。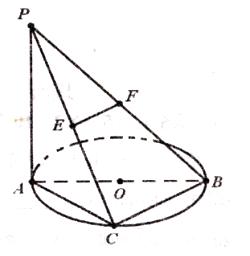
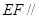 平面
平面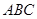 ;
;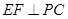 ;
;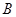 -
-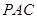 的体积。
的体积。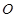 的面上有四点
的面上有四点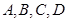 ,
,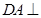 平面
平面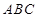 ,
,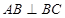 ,
,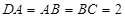 ,则球
,则球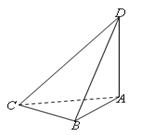
 是棱长为1的正方体,四棱锥
是棱长为1的正方体,四棱锥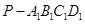 中,
中,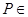 平面
平面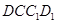 ,
,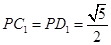 。
。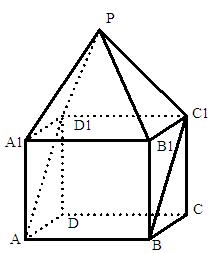
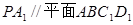
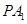 与平面
与平面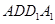 所成角的正切值。
所成角的正切值。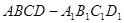 中,下列结论错误的是
中,下列结论错误的是 ∥平面
∥平面
 平面
平面

 与
与 所成的角是45º
所成的角是45º