题目内容
已知函数f(x)=4cosxsin(x+
)+k,其中k为常数.
(1)若x∈[0,
],f(x)的最大值为4,求k的值;
(2)将f(x)图象上的点的横坐标变为原来的λ(λ>1)倍,所得函数为g(x),设A、B是g(x)图象上任意两个相邻的最低点,线段AB与g(x)图象所围成的封闭图形的面为6π,点C是g(x)图象与y轴的交点,D是g(x)图象在y轴右侧且离y轴最近的一个对称中心,当
•
<0(O是坐标原点)时,求k的取值范围.
| π |
| 6 |
(1)若x∈[0,
| π |
| 2 |
(2)将f(x)图象上的点的横坐标变为原来的λ(λ>1)倍,所得函数为g(x),设A、B是g(x)图象上任意两个相邻的最低点,线段AB与g(x)图象所围成的封闭图形的面为6π,点C是g(x)图象与y轴的交点,D是g(x)图象在y轴右侧且离y轴最近的一个对称中心,当
| OC |
| OD |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(1)先化简函数的解析式为f(x)=4cosxsin(x+
)+k=2sin(2x+
)+k+1,再求出最值,令其等于4,即可得到k的方程求出它的值.
(2)本小题可由A、B是g(x)图象上任意两个相邻的最低点,线段AB与g(x)图象所围成的封闭图形的面为6π这一条件入手求出ω的值,由此可以确定出函数图象的大体位置,再由
•
<0得出k的不等式,解出其范围即可.
| π |
| 6 |
| π |
| 6 |
(2)本小题可由A、B是g(x)图象上任意两个相邻的最低点,线段AB与g(x)图象所围成的封闭图形的面为6π这一条件入手求出ω的值,由此可以确定出函数图象的大体位置,再由
| OC |
| OD |
解答:
解:(1)f(x)=4cosxsin(x+
)+k=2sin(2x+
)+k+1.
x∈[0,
],则2x+
∈[
,
],可得sin(2x+
)∈[-
,1].
又x∈[0,
],f(x)的最大值为4,可得k+3=4,解得k=1.
(2)由(1)知,f(x)=4cosxsin(x+
)+k=2sin(2x+
)+k+1.
∵A、B是g(x)图象上任意两个相邻的最低点,线段AB与g(x)图象所围成的封闭图形的面为6π,
∴|AB|×4=6π,解得|AB|=
π,即T=
π,故有ω=
=
,即g(x)=2sin(
x+
)+k+1
又点C是g(x)图象与y轴的交点,D是g(x)图象在y轴右侧且离y轴最近的一个对称中心,
•
<0
可得出k+1>0,故有k>-1.
k的取值范围k>-1.
| π |
| 6 |
| π |
| 6 |
x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
又x∈[0,
| π |
| 2 |
(2)由(1)知,f(x)=4cosxsin(x+
| π |
| 6 |
| π |
| 6 |
∵A、B是g(x)图象上任意两个相邻的最低点,线段AB与g(x)图象所围成的封闭图形的面为6π,
∴|AB|×4=6π,解得|AB|=
| 3 |
| 2 |
| 3 |
| 2 |
| 2π | ||
|
| 4 |
| 3 |
| 4 |
| 3 |
| π |
| 6 |
又点C是g(x)图象与y轴的交点,D是g(x)图象在y轴右侧且离y轴最近的一个对称中心,
| OC |
| OD |
可得出k+1>0,故有k>-1.
k的取值范围k>-1.
点评:本题考查三角恒等变换与数量积的意义,三角恒等变换是高考重要内容,它与向量的结合是近年高考中常出现的题型.

练习册系列答案
相关题目
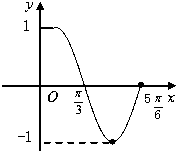 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤ 如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点.
如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点.