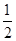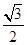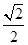题目内容
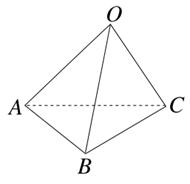
(本小题满分12分)如图,在多面体ABDEC中,AE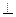 平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
(I)求证:EF//平面ABC;
(II)求证: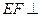 平面BCD;
平面BCD;
(III)求多面体ABDEC的体积。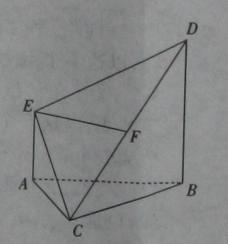
(1)找BC中点G点,连接AG,FG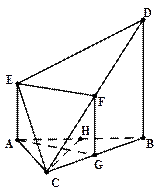
 F,G分别为DC,BC中点
F,G分别为DC,BC中点
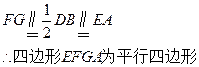
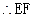 //AG
//AG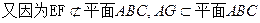
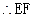 //平面ABC ……….4分
//平面ABC ……….4分
(2)因为 面
面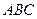 ,
,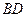 ∥
∥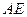
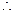 DB⊥平面ABC
DB⊥平面ABC
又∵DB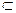 平面
平面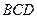
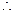 平面ABC⊥平面
平面ABC⊥平面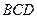
又∵G为 BC中点且AC=AB=BC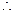 AG⊥BC
AG⊥BC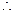 AG⊥平面
AG⊥平面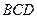 ,
,
又∵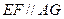
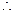
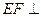 平面
平面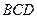 ……………………….8分
……………………….8分
(3)过C作CH⊥AB,则CH⊥平面ABDE且CH=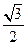
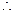
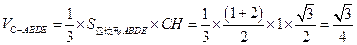 …………12分
…………12分
解析

练习册系列答案
相关题目
若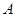 ,
,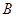 ,
,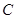 不共线,对于空间任意一点
不共线,对于空间任意一点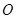 都有
都有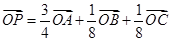 ,则
,则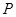 ,
,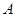 ,
,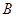 ,
,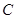 四点( )
四点( )
| A.不共面 | B.共面 | C.共线 | D.不共线 |
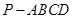 的底面
的底面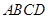 为矩形,且
为矩形,且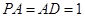 ,
,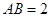 ,
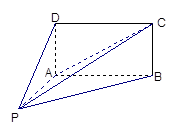
,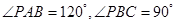 ,
,
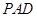 与平面
与平面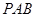 是否垂直?并说明理由;
是否垂直?并说明理由; 与平面
与平面
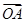 、
、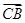 夹角θ的余弦值为( )
夹角θ的余弦值为( )