题目内容
设 .
.
(1)当 取到极值,求
取到极值,求 的值;
的值;
(2)当 满足什么条件时,
满足什么条件时, 在区间
在区间 上有单调递增的区间.
上有单调递增的区间.
 .
.(1)当
 取到极值,求
取到极值,求 的值;
的值;(2)当
 满足什么条件时,
满足什么条件时, 在区间
在区间 上有单调递增的区间.
上有单调递增的区间.(1)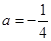 ;(2)
;(2)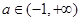 .
.
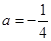 ;(2)
;(2)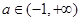 .
. 试题分析:(1)遵循“求导数、求驻点、讨论区间导数值的正负、确定极值”.
(2)要使
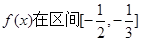 上有单调增区间,
上有单调增区间,也就是
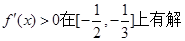 等价于
等价于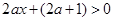 ,
,通过讨论
 三种情况,利用“分离参数法”,转化成不等式恒成立,通过确定函数的最值,得到
三种情况,利用“分离参数法”,转化成不等式恒成立,通过确定函数的最值,得到 的范围.
的范围.试题解析:(1)由题意知
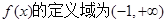 1分
1分且
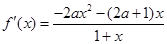 ,由
,由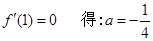
当
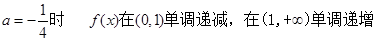
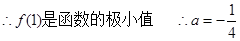 5分
5分(2)要使
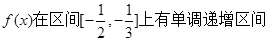
即
 7分
7分(i)当

(ii)当
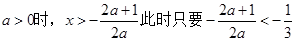 ,解得:
,解得: 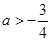
(iii)当
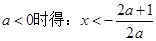 此时只要
此时只要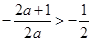 ,解得:
,解得: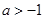 10分
10分综上得:
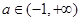 12分
12分
练习册系列答案
相关题目
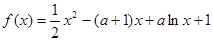
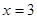 是
是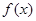 的极值点,求
的极值点,求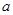 的范围,使得
的范围,使得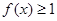 恒成立.
恒成立.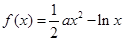 ,
,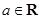 .
. 的单调区间;
的单调区间;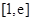 的最小值为
的最小值为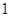 ,求
,求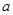 的值.
的值.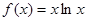 ,当
,当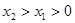 时,给出下列几个结论:
时,给出下列几个结论: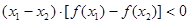 ;②
;②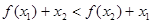 ;③
;③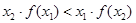 ;
;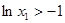 时,
时,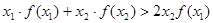 .
. 对任意的
对任意的 恒成立,则
恒成立,则 .
.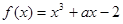 在区间
在区间 内是增函数,则实数
内是增函数,则实数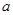 的取值范围是
的取值范围是 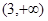
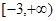
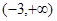
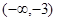
 的定义域为开区间
的定义域为开区间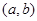 ,导函数
,导函数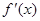 在
在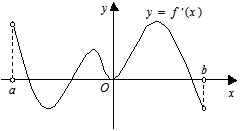
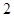 个
个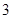 个
个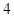 个
个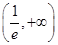
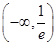
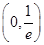
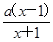 ,若函数f(x)在(0,+∞)上为增函数,则a的取值范围是________.
,若函数f(x)在(0,+∞)上为增函数,则a的取值范围是________.