题目内容
在三棱锥P-ABC中，若PA=PB=PC,则顶点P在底面ABC上的射影O必为△ABC的( )
| A．内心 | B．垂心 | C．重心 | D．外心 |
D
解析试题分析：因为在三棱锥P-ABC中， PA=PB=PC,所以顶点P在底面ABC上的射影O到底面三角形顶点距离相等，即0必为△ABC的外心，选D。
考点：本题主要考查三棱锥的几何特征。
点评：简单题，射影得到性质，斜线相等，射影也相等。
练习册系列答案
相关题目
一个几何体的三视图如右图所示，则它的体积为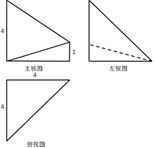
A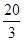． | B． |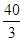
C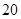． | D． |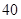
如图在棱长为5的正方体
中，
是棱
上的一条线段，且
，
是
中点，点
是棱
上动点，则四面体
的体积（ ）
| A．是变量且有最大值 | B．是变量且有最小值 |
| C．是变量且有最大值和最小值 | D．是常量 |
一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形. 则该几何体的体积为（ ）
| A．16 | B．48 |
| C．60 | D．96 |
一个与球心距离为1的平面截球所得的圆面积为
，则球的表面积为（ ）
A． | B． | C． | D． |
设有一几何体的三视图如下，则该几何体体积为（ ）
正视图 侧视图
俯视图（圆和正方形）
A．4+ | B．4+ | C．4+ | D．4+ |
的正方体上，分别用过共顶点的三条棱中点的平面截该正方形，则截去
个三棱锥后 ，剩下的几何体的体积是（ ）
