题目内容
如图在棱长为5的正方体 中,
中, 是棱
是棱 上的一条线段,且
上的一条线段,且 ,
, 是
是 中点,点
中点,点 是棱
是棱 上动点,则四面体
上动点,则四面体 的体积( )
的体积( )
| A.是变量且有最大值 | B.是变量且有最小值 |
| C.是变量且有最大值和最小值 | D.是常量 |
D
解析试题分析:连接QA,则QA到为Q点到AB的距离,又∵EF=2,故 为定值,又∵C1D1∥AB,则由线面平行的判定定理易得C1D1∥面QEF,又由P是棱C1D1上动点,故P点到平面QEF的距离也为定值,即四面体PQEF的底面积和高均为定值,故四面体PQEF的体积为定值。
为定值,又∵C1D1∥AB,则由线面平行的判定定理易得C1D1∥面QEF,又由P是棱C1D1上动点,故P点到平面QEF的距离也为定值,即四面体PQEF的底面积和高均为定值,故四面体PQEF的体积为定值。
考点:三棱锥的体积公式。
点评:本题考查的知识点是棱锥的体积,其中根据空间中点、线、面之间的位置关系及其性质,判断出四面体PQEF的底面积和高均为定值,是解答本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
用一个平面去截正方体,对于截面的边界,有以下图形:
①钝角三角形;②直角梯形;③菱形;④正五边形;⑤正六边形。
则不可能的图形的选项为( )
| A.③④⑤ | B.①②⑤ | C.①②④ | D.②③④ |
一简单组合体的三视图及尺寸如图示(单位: )则该组合体的体积为.
)则该组合体的体积为.


A.72000 | B.64000 |
C.56000 | D.44000 |
一个棱锥的三视图如图,则该棱锥的全面积(单位: )为
)为
A. | B. |
C. | D. |
若一个螺栓的底面是正六边形,它的主视图和俯视图如图所示,则它的体积是
A.27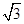 +12π +12π | B.9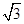 +12 +12 |
C.27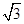 +3π +3π | D. 54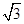 +3π +3π |
在长方体ABCD—A1B1C1D1中,有( )条棱所在的直线与直线AA1是异面直线且互相垂直。
| A.2 | B.4 | C.6 | D.8 |
在三棱锥P-ABC中,若PA=PB=PC,则顶点P在底面ABC上的射影O必为△ABC的( )
| A.内心 | B.垂心 | C.重心 | D.外心 |
下列判断正确的是( )
| A.棱柱中只能有两个面可以互相平行 |
| B.底面是正方形的直四棱柱是正四棱柱 |
| C.底面是正六边形的棱台是正六棱台 |
| D.底面是正方形的四棱锥是正四棱锥 |
 在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点
在空间直角坐标系中移动,但保持点A、B分别在x轴、y轴上移动,则点 到原点O的最远距离为( )
到原点O的最远距离为( ) B.
B. C.5 D.4
C.5 D.4