题目内容
如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的体积为
A. | B. |
C. | D. |
C
解析试题分析:观察三视图可知,该几何体是一个柱体,底面是一个半圆及一个等腰三角形,且半圆半径为1,等腰三角形底为半圆直径,其高为1.柱体的高为2,所以几何体体积为 =
= ,故选C。
,故选C。
考点:本题主要考查三视图,几何体的体积计算。
点评:基础题,三视图是高考必考题目,因此,要明确三视图视图规则,准确地还原几何体,明确几何体的特征,以便进一步解题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个棱锥的三视图如图,则该棱锥的全面积(单位: )为
)为
A. | B. |
C. | D. |
在三棱锥P-ABC中,若PA=PB=PC,则顶点P在底面ABC上的射影O必为△ABC的( )
| A.内心 | B.垂心 | C.重心 | D.外心 |
已知某个几何体的三视图如右图,根据图中标出的尺寸(单位: cm),可得这个几何体的体积是( )
A. cm3 cm3 | B. cm3 cm3 |
C. cm3 cm3 | D.2 cm3 |
三棱锥 的高为
的高为 ,若三个侧面两两垂直,则
,若三个侧面两两垂直,则 一定为△
一定为△ 的( )
的( )
| A.垂心 | B.外心 | C.内心 | D.重心 |
下列判断正确的是( )
| A.棱柱中只能有两个面可以互相平行 |
| B.底面是正方形的直四棱柱是正四棱柱 |
| C.底面是正六边形的棱台是正六棱台 |
| D.底面是正方形的四棱锥是正四棱锥 |
设四面体的六条棱的长分别为1,1,1,1,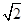 和
和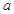 ,且长为
,且长为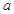 的棱与长为
的棱与长为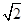 的棱异面,则
的棱异面,则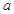 的取值范围是
的取值范围是
A.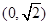 | B.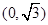 | C.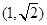 | D.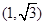 |
已知四棱锥 的三视图如图所示,则四棱锥
的三视图如图所示,则四棱锥 的四个侧面中面积最大的是
的四个侧面中面积最大的是
A. | B. | C. | D. |




