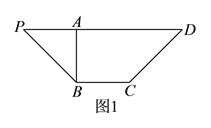
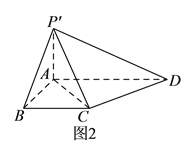
题目内容
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直,求
轴垂直,求![]() 的值;
的值;
(2)若![]() ,试探究函数
,试探究函数![]() 与
与![]() 的图象在其公共点处是否存在公切线.若存在,研究
的图象在其公共点处是否存在公切线.若存在,研究![]() 值的个数;,若不存在,请说明理由.
值的个数;,若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处不存在公切线,当
的图象在其公共点处不存在公切线,当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处存在公切线,且符合题意的
的图象在其公共点处存在公切线,且符合题意的![]() 的值有且仅有两个.
的值有且仅有两个.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,得到
,得到![]() ,依题意
,依题意![]() ,即可求解
,即可求解![]() 的值;(2)假设
的值;(2)假设![]() 的图象在其公共点
的图象在其公共点![]() 处存在公切线,分别求出导数,令
处存在公切线,分别求出导数,令![]() ,得
,得![]() ,讨论
,讨论![]() ,分别
,分别![]() ,
, ![]() ,令
,令![]() ,研究方程解的个数,可构造函数,运用都是求出单调区间,讨论函数的零点个数即可判断.
,研究方程解的个数,可构造函数,运用都是求出单调区间,讨论函数的零点个数即可判断.
试题解析:(1)当![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
依题意得![]() ,∴
,∴ ![]() .
.
(2)假设函数![]() 与
与![]() 的图象在其公共点
的图象在其公共点![]() 处存在公切线,
处存在公切线,
∵![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
由![]() 得
得![]() ,即
,即![]() ,
,
∴![]() ,故
,故![]() .
.
∵函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时, ![]() ,∴函数
,∴函数![]() 与
与![]() 的图象在其公共点处不存在公切线;
的图象在其公共点处不存在公切线;
当![]() 时,令
时,令![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() (
(![]() ).
).
下面研究满足此等式的![]() 的值的个数:
的值的个数:
设![]() ,则
,则![]() ,且
,且![]() ,方程
,方程![]() 化为
化为![]() ,
,
分别画出![]() 和
和![]() 的图象,
的图象,
当![]() 时,
时, ![]() ,
, ![]() ,
,
由函数图象的性质可得![]() 和
和![]() 的图象有且只有两个公共点(且均符合),
的图象有且只有两个公共点(且均符合),
∴方程![]() 有且只有两个根.
有且只有两个根.
综上,当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处不存在公切线;当
的图象在其公共点处不存在公切线;当![]() 时,函数
时,函数![]() 与
与![]() 的图象在其公共点处存在公切线,且符合题意的
的图象在其公共点处存在公切线,且符合题意的![]() 的值有且仅有两个.
的值有且仅有两个.
点晴:本题主要考查了导数在函数中的综合应用问题,其中解答中涉及到了利用导数求解曲线在某点处的切线方程,利用导数研究函数的单调性,利用函数的性质解决不等式、方程问题,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,本题的解答中认真审题,注意导数在函数中的合理应用,试题有一定的难度,属于难题.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 4 | 19 | 20 | 5 | 1 |
图1:乙套设备的样本的频率分布直方图

(1)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |||||||||||||
合格品 | |||||||||||||||
不合格品 | |||||||||||||||
合计 | ,求 |
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.