Question

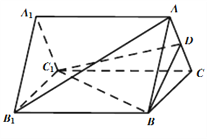
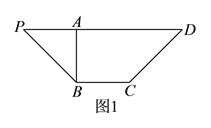
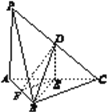
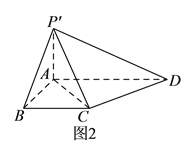
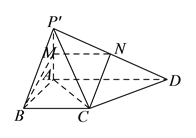
【题目】如图，等腰梯形中， ， 于点， ，且．沿把折起到的位置（如图），使．

（I）求证： 平面．

（II）求三棱锥的体积．

（III）线段上是否存在点，使得平面，若存在，指出点的位置并证明；若不存在，请说明理由．

Answer 1

【答案】（I）见解析；（II）；（III）存在， 为中点.

【解析】试题分析：（Ⅰ）推导出⊥AD，AB⊥．从而⊥面ABCD．进而⊥CD，再求出AC⊥CD．由此能证明CD⊥平面．

（Ⅱ）由VA-P'BC=VP'-ABC，能求出三棱锥A-P'BC的体积．

（Ⅲ）取P'A中点M，P'D中点N，连结BM，MN，NC，推导出四边形BCNM为平行四边形，由此能求出存在一点M，M为的中点，使得BM∥面CD．

试题解析：（I）∵，故，

∵在等腰梯形中， ，

∴在四棱锥中， ，

又∵，

∴平面，

∵平面，

∴，

∵等腰梯形中，

， ，

且，

∴， ， ，

∴，

∴，

∵，

∴平面．

（II），

∵平面，

∴，

．

（III）存在点， 为中点，使得平面，

证明：取， 中点为， ，

连接， ， ，

∵， 是， 中点，

∴，

∵，

∴，

∴是平行四边形，

∴，

∵面，

面，

∴平面．