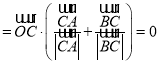Question

【题目】已知在直角坐标系xOy中，圆C的参数方程为为参数，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为．

1求圆C的普通方程和直线l的直角坐标方程；

2设M是直线l上任意一点，过M做圆C切线，切点为A、B，求四边形AMBC面积的最小值．

Answer 1

【答案】（1）圆的普通方程为.直线直角坐标方程 (2)

【解析】

（1）结合，消去参数，得到圆C的普通方程；结合

，代入，得到直线l的直角坐标方程。（2）计算，圆心C到该直线的距离，计算四边形AMBC的面积，计算最小值，即可。

（1）由得，

即圆的普通方程为.

由得，

即，由得直线直角坐标方程

（2）圆心到直线:的距离为

是直线上任意一点，则，

四边形面积……9分

四边形面积的最小值为