题目内容
某人有楼房一幢,室内面积共
解析：本题属于线性规划中的在人力、物力、资金等资源一定的条件下,如何使用它们来完成最多的任务的问题.若设大房间和小房间的数目分别为x、y,列出线性约束条件和目标函数,然后求目标函数的最大值.注意到这里的x、y都必须是非负整数,因此本题还是整点最优解问题,如何找到整点最优解是解决本题的关键所在.为了便于比较,我们分别用“局部微调法”和“小范围搜索法”进行求解.
解法一:“ 局部微调法”:?
设大房间和小房间分别为x、y间,则线性约束条件为
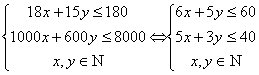
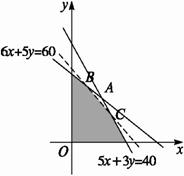
线性目标函数为z=200x+150y,作出可行域如图.?
解方程组
得到点
由于点A的坐标不是整数,故不是整数最优解,此时,z=
≈1 857.142 9.由可行域可知直线l:200x+150y=t应向下平移,故取z=1 857,此时200x+150y=1 857无整数解.根据整除性分析,将z=1 857降为1 800时,化为4x+3y=36,求得交点B、C的横坐标分别为x1=0,x2=4,∴0≤x≤4.?
当x=0时,y=12,z=1 800成立,故点(0,12)满足;?
当x=4时,y=
,非整点,故不满足;?
当x=1时,y=
,非整点;?
当x=2时,y=
,非整点;?
当x=3时,y=8,此时z=200x+150y=1 800.?
由以上讨论可知zmax=1 800,此时的最优解为(0,12),(3,8).?
答:应隔出大、小房间各3,8间或0,12间可获得最大利润,最大利润为1 800元.
解法二:“小范围搜索法”:?
设大房间和小房间的数目分别为x、y,则线性约束条件为?
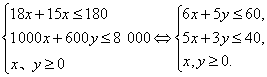
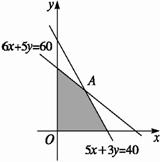
线性目标函数为z=200x+150y,作出可行域如图.(1)搜索一个可行域内邻近边界折线顶点的整点.?
解方程组
得到点A(
),由于点A的坐标不是整数,故不是最优解.要使目标函数取最大值,因此要寻找可行域右上侧靠近边界或边界上的整点.
与点A邻近的整点共有4个:(2,8),(2,9),(3,8),(3,9),显然点(2,8)是可行域内的整点,点(3,9)不是可行域内的整点,记点(a,b)处的目标函数值为z(a,b),由于:z(2,9)＞z(2,8),故还应检验点(2,9),(3,8)是否在可行域内.?
注意到目标函数z=200x+150y=150(x+y)+50x,而2+9=3+8,故必有z(3,8)＞z(2,9),所以应先检验点(3,8)是否在可行域内.观察与计算都表明该点在可行域内.记点(3,8)为B,B即为搜索到的可行域内邻近边界折线顶点的整点.?
(2)作出可行域内的小范围搜索区域.?
算得z(3,8)=1 800,过点B作直线200x+150y=1 800
4x+3y=36.?
解方程组
得C(0,12),为整点.?
解方程组
得D(
),则△ACD即是新的搜索区.在△ACD内(包括边界)内可以搜索到全部最优解整点,该搜索区域比可行域大大缩小.?
(3)在△ACD(包括边界)内搜索最优解整点.?
通过观察图形可知△ACD(包括边界)内整点只有B(3,8),C(0,12),由于B、C在一直线上,所以z(3,8)=z(0,12)=1 800.?
B、C均为最优解整点,1 800为目标函数的最大值.?
答:应隔出大、小房间各3,8间或0,12间可获得最大利润为1 800元.
期末宝典单元检测分类复习卷系列答案
某人有楼房一幢，室内面积共计180m2，拟分割成两类房间作为旅游客房，大房间每间面积为18m2，可住游客5名，每名游客每天住宿费40元；小房间每间面积为15m2，可以住游客3名，每名游客每天住宿费50元；装修大房间每间需要1000元，装修小房间每间需要600元．如果他只能筹款8000元用于装修，且假定游客能住满客房，他应隔出大房间和小房间各多少间，才能获得最大收益？