题目内容
已知函数f(x)=
x3-ax2-3x(x∈R)在点A(1,f(1))处的切线达到斜率的最小值.
(Ⅰ)求函数f(x)的解析式及函数f(x)在A(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)的单调区间和极值.
| 1 |
| 3 |
(Ⅰ)求函数f(x)的解析式及函数f(x)在A(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)的单调区间和极值.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求出原函数的导函数f′(x)=x2-2ax-3=(x-a)2-a2-3,再根据f(x)在点A(1,f(1))处的切线达到斜率的最小值可得a=1,则函数解析式可求,进一步求得f(1)与f′(1),则f(x)在A(1,f(1))处的切线方程可求;
(Ⅱ)求出原函数的导函数,求得导函数的零点,由导函数的零点对定义域分段,利用导函数在各区间段内的符号判断原函数的单调性,从而求得函数的极值.
(Ⅱ)求出原函数的导函数,求得导函数的零点,由导函数的零点对定义域分段,利用导函数在各区间段内的符号判断原函数的单调性,从而求得函数的极值.
解答:
解:(Ⅰ)由f(x)=
x3-ax2-3x,得f′(x)=x2-2ax-3=(x-a)2-a2-3,
∵函数f(x)=
x3-ax2-3x(x∈R)在点A(1,f(1))处的切线达到斜率的最小值,
则a=1,
∴f(x)=
x3-x2-3x;
此时f(1)=
-1-3=-
,f′(1)=-4,
∴函数f(x)在A(1,f(1))处的切线方程为y+
=-4(x-1),即12x+3y-1=0;
(Ⅱ)由f(x)=
x3-x2-3x,得f′(x)=x2-2x-3=(x+1)(x-3),
当x∈(-∞,-1),(3,+∞)时,f′(x)>0,函数为增函数;
当x∈(-1,3)时,f′(x)<0,函数为减函数.
∴函数f(x)的增区间为∈(-∞,-1),(3,+∞);减区间为(-1,3);
当x=-1时,函数f(x)有极大值为f(-1)=
×(-1)3-(-1)2-3×(-1)=
;
当x=3时,函数f(x)有极小值为f(3)=
×33-32-3×3=-9.
| 1 |
| 3 |
∵函数f(x)=
| 1 |
| 3 |
则a=1,
∴f(x)=
| 1 |
| 3 |
此时f(1)=
| 1 |
| 3 |
| 11 |
| 3 |
∴函数f(x)在A(1,f(1))处的切线方程为y+
| 11 |
| 3 |
(Ⅱ)由f(x)=
| 1 |
| 3 |
当x∈(-∞,-1),(3,+∞)时,f′(x)>0,函数为增函数;
当x∈(-1,3)时,f′(x)<0,函数为减函数.
∴函数f(x)的增区间为∈(-∞,-1),(3,+∞);减区间为(-1,3);
当x=-1时,函数f(x)有极大值为f(-1)=
| 1 |
| 3 |
| 5 |
| 3 |
当x=3时,函数f(x)有极小值为f(3)=
| 1 |
| 3 |
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,训练了函数极值的求法,是中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知数列{an}是等差数列,且an=2n+1,则公差d=( )
| A、1 | B、2 | C、3 | D、-2 |
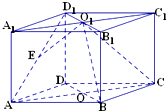 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC与BD交于点O,A1C1与B1D1交于点O1,E为AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC与BD交于点O,A1C1与B1D1交于点O1,E为AD1的中点.