题目内容
已知函数 ,其中
,其中 .
.
(1)若曲线 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式;
(2)讨论函数 的单调性;
的单调性;
(3)若对于任意的 ,不等式
,不等式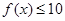 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
(1)函数 的解析式为
的解析式为 ;(2)当
;(2)当 时,
时, 在
在 ,
, 内是增函数;当
内是增函数;当 时
时 在
在 ,
,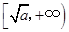 内是增函数,在
内是增函数,在 ,
, 内是减函数;(3)
内是减函数;(3) .
.
解析试题分析:(1)先求出导函数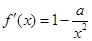 ,进而根据曲线
,进而根据曲线 在点
在点 处的切线方程为
处的切线方程为 得到
得到 即
即 ,从中可求解出
,从中可求解出 的值,进而可确定函数
的值,进而可确定函数 的解析式;(2)针对导函数,对
的解析式;(2)针对导函数,对 分
分 、
、 两类,由导数大于零求出函数的单调增区间,由导数小于零可求出函数的单调递减区间;(3)要使对于任意的
两类,由导数大于零求出函数的单调增区间,由导数小于零可求出函数的单调递减区间;(3)要使对于任意的 ,不等式
,不等式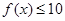 在
在 上恒成立,只须
上恒成立,只须 ,由(2)的讨论,确定函数
,由(2)的讨论,确定函数 ,进而得到不等式
,进而得到不等式 即
即 ,该不等式组对任意的
,该不等式组对任意的 成立,从中可求得
成立,从中可求得 .
.
(1)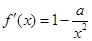 ,由导数的几何意义得
,由导数的几何意义得 ,于是
,于是
由切点 在直线
在直线 上可得
上可得 ,解得
,解得
所以函数 的解析式为
的解析式为 3分
3分
(2)因为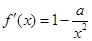
当 时,显然
时,显然 ,这时
,这时 在
在 ,
, 内是增函数
内是增函数
当 时,令
时,令 ,解得
,解得
当 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:









 练习册系列答案
练习册系列答案
经纶学典默写达人系列答案
名师讲坛1课1练系列答案
名师导航同步练与测系列答案
课堂感悟系列答案
经纶学典中考分类精华集系列答案
启东系列江苏省13大市中考真题汇编系列答案
江苏13大市中考20套卷系列答案
润学书业亮点给力江苏中考48套系列答案
锁定中考江苏十三大市中考试卷汇编系列答案
名校压轴题系列答案
相关题目
 .
. 的方程f(x)=a在区间
的方程f(x)=a在区间 上有三个根,求a的取值范围.
上有三个根,求a的取值范围.
 的单调区间和极值;
的单调区间和极值; ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围
的取值范围 .
. 的单调区间;
的单调区间; 为
为 个零点,证明:对一切
个零点,证明:对一切 ,有
,有 .
. ,函数
,函数 .
.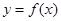 的极值点,求
的极值点,求 的值;
的值; ,若
,若 ≤0对一切
≤0对一切 都成立,求
都成立,求 .
. 时,求
时,求 的单调区间;
的单调区间; 时,若存在
时,若存在 , 使得
, 使得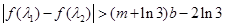 成立,求实数
成立,求实数 的取值范围.
的取值范围. =
= ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
 .
. 时,求函数
时,求函数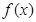 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最小值
上的最小值 和最大值
和最大值 .
. ,函数
,函数 的导函数
的导函数 ,且
,且 ,其中
,其中 为自然对数的底数.
为自然对数的底数. 的极值;
的极值; ,使得不等式
,使得不等式 成立,试求实数
成立,试求实数 的取值范围;
的取值范围;