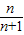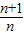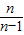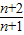题目内容
设f(x)=a•qx(a,q是正数,q≠1),不等的正整数m、k、h满足k2=mh,试比较[f(m)]| 1 |
| m |
| 1 |
| h |
| 2 |
| k |
分析:将f(x)=a•qx代入到[f(m)]
[f(h)]
与[f(k)]
中所得结果相比消去q,得到m,n,k的关系式,再由基本不等式的判断
+
与
的大小,结合指数函数的知识可判断出大小关系.
| 1 |
| m |
| 1 |
| h |
| 2 |
| k |
| 1 |
| m |
| 1 |
| n |
| 2 |
| k |
解答:解:[f(m)]
[f(h)]
=a
+
•q2>0,[f(k)]
=a
•q2>0,
=a
+
-
,
因为m,n是不等的正整数,则
+
>2
=
当a>1时,[f(m)]
[f(h)]
>[f(k)]
,
当a=1时,[f(m)]
[f(h)]
=[f(k)]
,
当a<1时,[f(m)]
[f(h)]
<[f(k)]
,
| 1 |
| m |
| 1 |
| h |
| 1 |
| m |
| 1 |
| h |
| 2 |
| k |
| 2 |
| k |
a
| ||||
a
|
| 1 |
| m |
| 1 |
| h |
| 2 |
| k |
因为m,n是不等的正整数,则
| 1 |
| m |
| 1 |
| h |
|
| 2 |
| k |
当a>1时,[f(m)]
| 1 |
| m |
| 1 |
| h |
| 2 |
| k |
当a=1时,[f(m)]
| 1 |
| m |
| 1 |
| h |
| 2 |
| k |
当a<1时,[f(m)]
| 1 |
| m |
| 1 |
| h |
| 2 |
| k |
点评:本题主要考查 基本不等式的应用和指数函数的性质.考查基础知识的综合应用和灵活能力,基本不等式在高考中应用比较广泛,尤其是在解决最值和比较大小中更是占据了举足轻重的地位.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
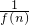 }的前n项的和为
}的前n项的和为


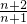
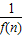 }的前n项的和为( )
}的前n项的和为( )