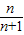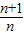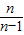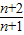题目内容
设函数f(x)=xp+qx的导函数f′(x)=2x+1,则数列{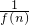 }的前n项的和为
}的前n项的和为
- A.

- B.

- C.

- D.
A
分析:利用f′(x)=(xp)′+(qx)′=pxp-1+q=2x+1,可求得p=2,q=1.从而得f(n)=n2+n,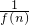 =
= -
- ,用累加法即可求其和.
,用累加法即可求其和.
解答:∵f′(x)=(xp)′+(qx)′=pxp-1+q=2x+1,
∴p=2,q=1,
∴f(n)=n2+n,
∴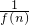 =
= -
- ,
,
∴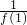 +
+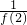 +…+
+…+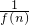 =(1-
=(1- )+(
)+( -
- )+…+(
)+…+( -
- )=1-
)=1- =
= .
.
故选A.
点评:本题考查数列的求和,着重考察导数的运算及裂项法、累加法求和,属于中档题.
分析:利用f′(x)=(xp)′+(qx)′=pxp-1+q=2x+1,可求得p=2,q=1.从而得f(n)=n2+n,
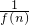 =
= -
- ,用累加法即可求其和.
,用累加法即可求其和.解答:∵f′(x)=(xp)′+(qx)′=pxp-1+q=2x+1,
∴p=2,q=1,
∴f(n)=n2+n,
∴
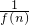 =
= -
- ,
,∴
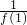 +
+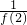 +…+
+…+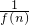 =(1-
=(1- )+(
)+( -
- )+…+(
)+…+( -
- )=1-
)=1- =
= .
.故选A.
点评:本题考查数列的求和,着重考察导数的运算及裂项法、累加法求和,属于中档题.

练习册系列答案
相关题目
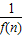 }的前n项的和为( )
}的前n项的和为( )