题目内容
如图,正四棱锥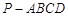 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
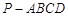 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
A. | B. |
C. | D. |
D
试题分析:由于正四棱锥
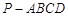 的所有棱长相等,设为2,BE=
的所有棱长相等,设为2,BE= ,,EO=1,OB=
,,EO=1,OB= ,E为PC的中点,那么可知连接AC,BD的交点O,则将BE平移到PA,则在三角形EOB中,利用三边长度可知异面直线BE与PA所成角的余弦值是
,E为PC的中点,那么可知连接AC,BD的交点O,则将BE平移到PA,则在三角形EOB中,利用三边长度可知异面直线BE与PA所成角的余弦值是 ,故选D.
,故选D.点评:求解异面直线的所成的角,一般采用平移法,放在一个三角形中来求解运算,属于基础题。

练习册系列答案
相关题目
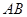 、
、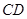 在原正方体的位置关系是( )
在原正方体的位置关系是( )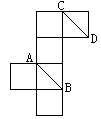
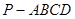 的底面是边长为6的正方形,侧棱
的底面是边长为6的正方形,侧棱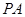 的长为8,且垂直于底面,点
的长为8,且垂直于底面,点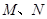 分别是
分别是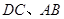 的中点.求
的中点.求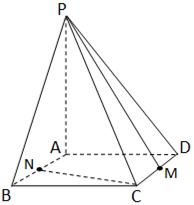
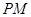 与
与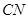 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);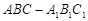 中,△
中,△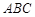 为等腰直角三角形,∠
为等腰直角三角形,∠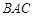 =
=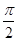 ,且
,且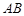 =
=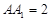 ,
,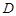 、
、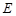 、
、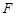 分别为
分别为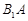 、
、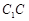 、
、 的中点.
的中点.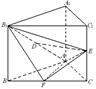
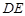 ∥平面
∥平面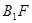 ⊥平面
⊥平面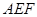 ;
;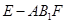 的体积.
的体积.

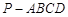 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形, 是棱
是棱 上的动点.
上的动点.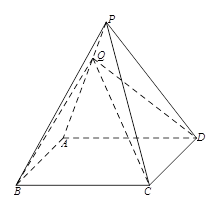
 是
是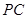 //平面
//平面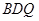 ;
;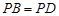 ,求证:
,求证: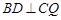 ;
;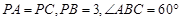 ,求四棱锥
,求四棱锥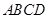 所在平面与平面
所在平面与平面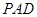 垂直,
垂直,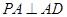 ,且
,且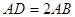 ,
,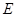 为
为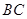 上的动点.
上的动点.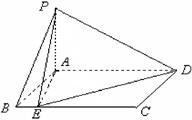
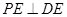 ;
;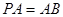 ,在线段
,在线段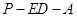 的大小为
的大小为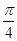 . 若存在,确定点E的位置,若不存在,说明理由.
. 若存在,确定点E的位置,若不存在,说明理由.