题目内容
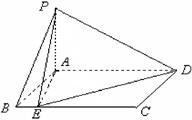
(本小题满分12分)如图,矩形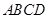 所在平面与平面
所在平面与平面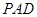 垂直,
垂直,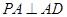 ,且
,且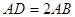 ,
,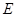 为
为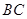 上的动点.
上的动点.
(Ⅰ)当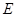 为
为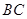 的中点时,求证:
的中点时,求证: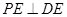 ;
;
(Ⅱ)若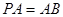 ,在线段
,在线段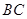 上是否存在点E,使得二面角
上是否存在点E,使得二面角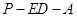 的大小为
的大小为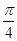 . 若存在,确定点E的位置,若不存在,说明理由.
. 若存在,确定点E的位置,若不存在,说明理由.
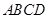 所在平面与平面
所在平面与平面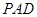 垂直,
垂直,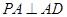 ,且
,且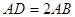 ,
,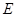 为
为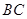 上的动点.
上的动点.
(Ⅰ)当
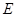 为
为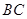 的中点时,求证:
的中点时,求证: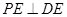 ;
;(Ⅱ)若
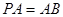 ,在线段
,在线段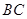 上是否存在点E,使得二面角
上是否存在点E,使得二面角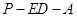 的大小为
的大小为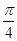 . 若存在,确定点E的位置,若不存在,说明理由.
. 若存在,确定点E的位置,若不存在,说明理由.(1)根据已知条件当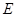 为
为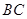 中点时,
中点时,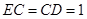 ,
,
从而 为等腰直角三角形,∴
为等腰直角三角形,∴ ,同理可得
,同理可得 ,∴
,∴ ,
,
于是 ,再结合又平面
,再结合又平面 平面
平面 ,得到
,得到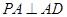
 平面
平面 得到证明。 (2) 点
得到证明。 (2) 点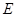 在线段BC上距B点
在线段BC上距B点 处
处
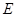 为
为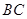 中点时,
中点时,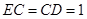 ,
, 从而
 为等腰直角三角形,∴
为等腰直角三角形,∴ ,同理可得
,同理可得 ,∴
,∴ ,
,于是
 ,再结合又平面
,再结合又平面 平面
平面 ,得到
,得到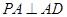
 平面
平面 得到证明。 (2) 点
得到证明。 (2) 点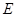 在线段BC上距B点
在线段BC上距B点 处
处试题分析:方法一:不妨设
 ,则
,则 .
.(Ⅰ)证明:当
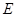 为
为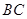 中点时,
中点时,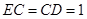 ,
, 从而
 为等腰直角三角形,∴
为等腰直角三角形,∴ ,
,同理可得
 ,∴
,∴ ,
,于是
 ,
, 又平面
 平面
平面 ,
,平面
 平面
平面 ,
,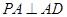
 平面
平面 ,
, 
∴

 ,又
,又 ,∴
,∴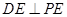 .………………6分
.………………6分(Ⅱ)若线段
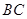 上存在点
上存在点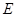 ,使二面角
,使二面角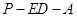 为
为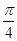 。
。过点
 作
作 于
于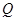 ,连接
,连接 ,由⑴
,由⑴ 所以
所以

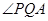 为二面角
为二面角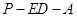 的平面角,
的平面角, …………………………..8分
…………………………..8分设
 , 则
, 则 中
中 ,在
,在 中由
中由 ,
, 得
得 ,则
,则 ,在
,在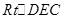 中
中  ,所以
,所以 ,所以线段
,所以线段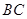 上存在点
上存在点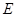 ,当
,当 时,二面角
时,二面角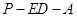 为
为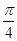 。 .12分
。 .12分方法二:∵平面
 平面
平面 ,平面
,平面 平面
平面 ,
,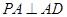
 平面
平面 ,
,以
 为原点,
为原点,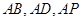 所在直线为
所在直线为 轴,建立空间直角坐标系如图.
轴,建立空间直角坐标系如图. 
(Ⅰ)不妨设
 ,AB=1
,AB=1 则
 ,
,从而
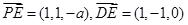 ,…………………………4分
,…………………………4分于是
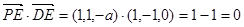 ,
,所以
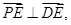 所以
所以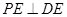 ………………………………6分
………………………………6分(Ⅱ)设
 ,则
,则 ,
, .……………………………………8分
.……………………………………8分易知向量
 为平面
为平面 的一个法向量.设平面
的一个法向量.设平面 的法向量
的法向量 ,
,则
 即
即 ,解得
,解得 ,令
,令 则
则 ,
, ,
,从而
 ,……………………………………………10分
,……………………………………………10分依题意
 ,即
,即 ,
,解得
 (舍去),
(舍去),
所以点
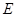 在线段BC上距B点
在线段BC上距B点 处..………………………………………12分
处..………………………………………12分点评:解决该试题的关键是能熟练的运用已学的线面垂直的判定定理和性质定理来证明线线垂直,同时用平面的法向量来求解二面角的大小。属于中档题。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
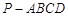 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是( )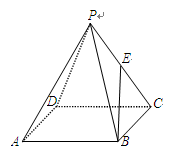




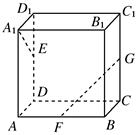
 中,
中, //
// ,
, ,
,  ,
, 平面
平面 ,
, .
. 
 平面
平面 ,求证:
,求证: ;
; 平面
平面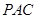 ;
; 为线段
为线段 上一点,且直线
上一点,且直线 与平面
与平面 ,求
,求 的值.
的值. 和平面
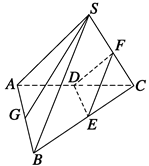
和平面 ,下列四个命题中,正确的是( )
,下列四个命题中,正确的是( ) 则
则


 则
则


 是两不同直线,
是两不同直线,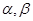 是两不同平面,则下列命题错误的是
是两不同平面,则下列命题错误的是 ,
, ∥
∥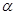 ,则
,则
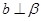 ,
,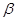 ,则
,则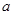 ∥
∥ ,则
,则
 、b是两条不同的直线,
、b是两条不同的直线, 、
、 是两个不同的平面,则下列四个命题中正确的是( )
是两个不同的平面,则下列四个命题中正确的是( )