题目内容
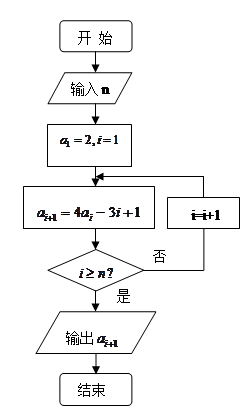
(6分)已知数列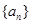 满足如图所示的程序框图。
满足如图所示的程序框图。
(I)写出数列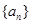 的一个递推关系式;并求数列
的一个递推关系式;并求数列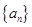 的通项公式
的通项公式
(Ⅱ)设数列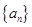 的前
的前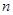 项和
项和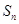 ,证明不等式
,证明不等式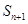 ≤
≤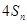 ,对任意
,对任意 皆成立.
皆成立.
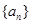 满足如图所示的程序框图。
满足如图所示的程序框图。
(I)写出数列
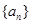 的一个递推关系式;并求数列
的一个递推关系式;并求数列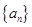 的通项公式
的通项公式(Ⅱ)设数列
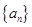 的前
的前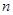 项和
项和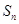 ,证明不等式
,证明不等式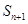 ≤
≤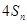 ,对任意
,对任意 皆成立.
皆成立.(Ⅰ) ,
, ,
, ;(Ⅱ)见解析。
;(Ⅱ)见解析。
 ,
, ,
, ;(Ⅱ)见解析。
;(Ⅱ)见解析。本试题主要是考查了框图的知识,以及数列的通项公式和求和的综合运用。
(1)由程序框图可知, 数列{an}的一个递推关系式:
 ,
,
 ,
, .
.
又 ,所以数列
,所以数列 是首项为
是首项为 ,且公比为
,且公比为 的等比数列,可得结论。
的等比数列,可得结论。
(2)由(Ⅰ)可知数列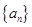 的前
的前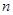 项和
项和 对任意的
对任意的 ,
,
所以不等式 ,对任意
,对任意 皆成立.只要作差可以得到参数的取值范围。
皆成立.只要作差可以得到参数的取值范围。
解(Ⅰ)由程序框图可知, 数列{an}的一个递推关系式:
 ,
, …………………………………………1分
…………………………………………1分
 ,
, .
.
又 ,所以数列
,所以数列 是首项为
是首项为 ,且公比为
,且公比为 的等比数列,
的等比数列,
 …………………………………………3分
…………………………………………3分
(Ⅱ)由(Ⅰ)可知数列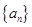 的前
的前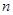 项和
项和 ……………4分
……………4分
对任意的 ,
,


所以不等式 ,对任意
,对任意 皆成立.………………………………6分
皆成立.………………………………6分
(1)由程序框图可知, 数列{an}的一个递推关系式:
 ,
,
 ,
, .
.又
 ,所以数列
,所以数列 是首项为
是首项为 ,且公比为
,且公比为 的等比数列,可得结论。
的等比数列,可得结论。(2)由(Ⅰ)可知数列
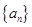 的前
的前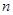 项和
项和 对任意的
对任意的 ,
,所以不等式
 ,对任意
,对任意 皆成立.只要作差可以得到参数的取值范围。
皆成立.只要作差可以得到参数的取值范围。解(Ⅰ)由程序框图可知, 数列{an}的一个递推关系式:
 ,
, …………………………………………1分
…………………………………………1分 ,
, .
.又
 ,所以数列
,所以数列 是首项为
是首项为 ,且公比为
,且公比为 的等比数列,
的等比数列, …………………………………………3分
…………………………………………3分(Ⅱ)由(Ⅰ)可知数列
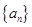 的前
的前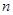 项和
项和 ……………4分
……………4分对任意的
 ,
,

所以不等式
 ,对任意
,对任意 皆成立.………………………………6分
皆成立.………………………………6分
练习册系列答案
相关题目
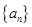 中,
中,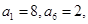 且满足
且满足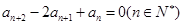 .
.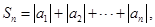 求
求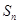 .
.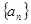 的前
的前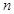 项和为
项和为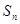 ,已知
,已知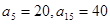 ,
,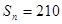 ,求
,求 中,
中, ,其前n项
,其前n项 ,则n=
,则n= 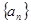 是等差数列,数列
是等差数列,数列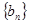 的前n项和
的前n项和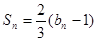 ,若
,若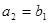 ,
,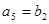 ,(1)求数列
,(1)求数列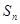 .
.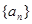 是公差为正数的等差数列,若
是公差为正数的等差数列,若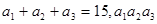 =80,则
=80,则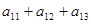 =
=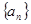 是等差数列,
是等差数列,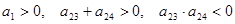 ,则使前
,则使前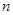 项和
项和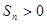 成立的最大正数
成立的最大正数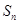 是等差数列
是等差数列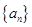 的前
的前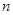 项和,已知
项和,已知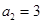 ,
,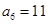 ,则
,则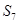 等于( )
等于( )