题目内容
设函数 ,曲线
,曲线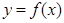 过点
过点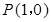 ,且在点
,且在点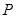 处的切线斜率为2.
处的切线斜率为2.
(Ⅰ)求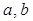 的值;
的值;
(Ⅱ)求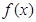 的极值点;
的极值点;
(Ⅲ)对定义域内任意一个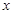 ,不等式
,不等式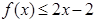 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。
 ,曲线
,曲线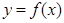 过点
过点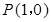 ,且在点
,且在点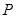 处的切线斜率为2.
处的切线斜率为2.(Ⅰ)求
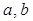 的值;
的值;(Ⅱ)求
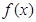 的极值点;
的极值点;(Ⅲ)对定义域内任意一个
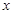 ,不等式
,不等式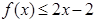 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。(Ⅰ)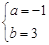 ;(Ⅱ)
;(Ⅱ)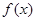 只有极大值点,且极大值点为
只有极大值点,且极大值点为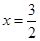 ;(Ⅲ)见解析。
;(Ⅲ)见解析。
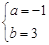 ;(Ⅱ)
;(Ⅱ)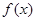 只有极大值点,且极大值点为
只有极大值点,且极大值点为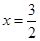 ;(Ⅲ)见解析。
;(Ⅲ)见解析。试题分析:(Ⅰ)∵
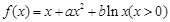
∴
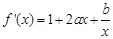 ...................1分
...................1分∵
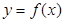 在点
在点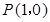 处的切线斜率为2
处的切线斜率为2∴
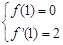 即
即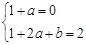 ......................2分
......................2分故
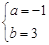 ..............................3分
..............................3分(Ⅱ)∵
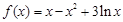 (
(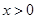 )
)得
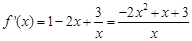 ................4分
................4分即
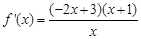
由
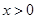 可得,
可得, 当
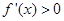 时,
时,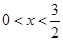 ...................5分
...................5分当
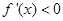 时,
时,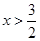 ............................6分
............................6分列表可得:
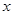 | 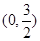 | 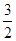 | 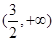 |
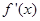 | + | 0 | — |
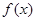 | ↗ | | ↙ |
故
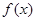 只有极大值点,且极大值点为
只有极大值点,且极大值点为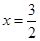 ..........................8分
..........................8分(Ⅲ)令
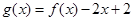 ,得
,得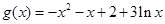 (
(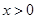 )............9分
)............9分∴
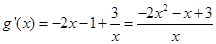
即
 ..................10分
..................10分由
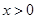 可得,
可得, 当
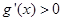 时,
时,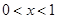
当
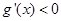 时,
时,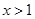 .........................11分
.........................11分列表可得:
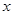 | 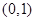 | 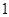 | 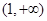 |
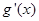 | + | 0 | — |
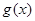 | ↗ | 0 | ↙ |
由表可知
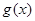 的最大值为
的最大值为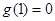
即
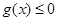 恒成立
恒成立故
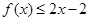 恒成立.......................12分
恒成立.......................12分点评:极值点的导数为零,但导数为零的点不一定是极值点。因此在求极值点的时候仅仅由
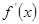 =0得到的点不一定是极值点,而应该加以验证。
=0得到的点不一定是极值点,而应该加以验证。
练习册系列答案
相关题目
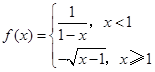 ,
,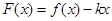 ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性.  在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间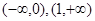 上是减函数,又
上是减函数,又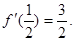
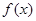 的解析式;
的解析式;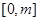 (m>0)上恒有
(m>0)上恒有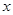 成立,求m的取值范围.
成立,求m的取值范围.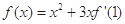 ,则
,则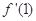 为
为 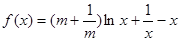 ,其中常数
,其中常数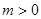 .
.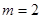 时,求函数
时,求函数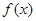 的极大值;
的极大值;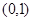 上的单调性;
上的单调性;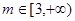 时,曲线
时,曲线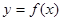 上总存在相异两点
上总存在相异两点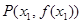 ,
,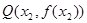 ,使得曲线
,使得曲线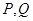 处的切线互相平行,求
处的切线互相平行,求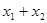 的取值范围.
的取值范围.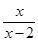 在点(1,-1)处的切线方程为
在点(1,-1)处的切线方程为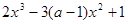 ,其中
,其中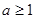
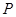 (-1,2)且与曲线
(-1,2)且与曲线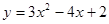 在点
在点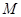 (1,1)处的切线平行的直线方程是______.
(1,1)处的切线平行的直线方程是______.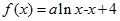 ,(
,(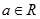 ),曲线
),曲线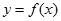 在点
在点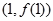 处的切线垂直于
处的切线垂直于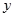 轴.
轴.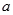 的值;
的值;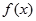 的极值。
的极值。