题目内容
 已知函数f(x)=2cos(2x+
已知函数f(x)=2cos(2x+| π |
| 3 |
(Ⅰ)先列表,再用“五点法”画出该函数在一个周期内的简图;
(Ⅱ)写出该函数在[0,π]的单调递减区间.
考点:复合三角函数的单调性,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:根据五点法作图的方法先取值,然后描点即可得到图象.
解答:
解:(I)列表如下:
后描点并画图,简图如右图一个周期:

(II)由2kπ≤2x+
≤2kπ+π解得kπ-
x≤kπ+
,k∈Z
和[0,π]取交集可得原函数的递减区间[0,
],[
π,π]
| x | -
|
|
|
|
| ||||||||||
2x+
|
0 |
|
π |
|
2π | ||||||||||
cos(2x+
|
1 | 0 | -1 | 0 | 1 | ||||||||||
y=2cos(2x+
|
3 | 1 | -1 | 1 | 3 |

(II)由2kπ≤2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
和[0,π]取交集可得原函数的递减区间[0,
| π |
| 3 |
| 5 |
| 6 |
点评:本题考查三角函数的图象的作法,利用五点法是解决三角函数图象的基本方法,考查正弦函数的单调区间的确定,属中档题.

练习册系列答案
相关题目
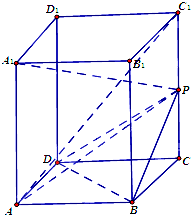 如图,在直四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱C1C垂直于底面ABCD,且C1C=2,点P是侧棱C1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱C1C垂直于底面ABCD,且C1C=2,点P是侧棱C1C的中点.