题目内容
求证:tanα+| 1 |
| 2 |
| α |
| 2 |
| 1 |
| 4 |
| α |
| 4 |
| 1 |
| 2n-1 |
| α |
| 2n-1 |
| 1 |
| 2n-1 |
| α |
| 2n-1 |
分析:通过数学归纳法来证明.先证当n=1时成立,假设当n=k时成立,然后当n=k+1时,代入n=k时的结果用二倍角公式化简整理可得证.
解答:证明:当n=1时,左边=tanα,
右边=cotα-2cot2α=
-2×
=
=tanα=左边,成立
假设当n=k时成立,即tanα+
tan
+
tan
+…+
tan
=
cot
-2cot2α成立
当n=k+1时,左边=tanα+
tan
+
tan
+…+
tan
+
tan
=
cot
-2cot2α+
tan
=
[
+
(
)]-2cot2α
=
(
+
)-2cot2α
=
(
)-2cot2α=
cot
-2cot2α=右边
得证.
右边=cotα-2cot2α=
| cosα |
| sinα |
| cos2α-sin2α |
| 2sinαcosα |
| sin2α |
| sinαcosα |
假设当n=k时成立,即tanα+
| 1 |
| 2 |
| α |
| 2 |
| 1 |
| 4 |
| α |
| 4 |
| 1 |
| 2k-1 |
| α |
| 2k-1 |
| 1 |
| 2k-1 |
| α |
| 2k-1 |
当n=k+1时,左边=tanα+
| 1 |
| 2 |
| α |
| 2 |
| 1 |
| 4 |
| α |
| 4 |
| 1 |
| 2k-1 |
| α |
| 2k-1 |
| 1 |
| 2k |
| α |
| 2k |
=
| 1 |
| 2k-1 |
| α |
| 2k-1 |
| 1 |
| 2k |
| α |
| 2k |
| 1 |
| 2k-1 |
cos
| ||
sin
|
| 1 |
| 2 |
sin
| ||
cos
|
=
| 1 |
| 2k-1 |
cos2
| ||||
2sin
|
sin2
| ||||
2sin
|
=
| 1 |
| 2k-1 |
cos2
| ||||
2sin
|
| 1 |
| 2k |
| α |
| 2k |
得证.
点评:本题主要考查二倍角公式、同角三角函数的基本关系.对于三角函数的公式一定要强化记忆,才能熟练做题.

练习册系列答案
相关题目
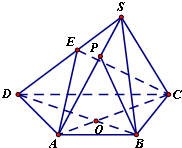 如图,四棱锥S-ABCD,底面ABCD是等腰梯形,AB∥DC,tan∠ACB=
如图,四棱锥S-ABCD,底面ABCD是等腰梯形,AB∥DC,tan∠ACB= 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CD,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CD,⊙O交直线OB于E,D,连接EC,CD.