题目内容
若
=2，则tan(α+
)等于（ ）
| sinα-cosα |
| sinα+cosα |
| π |
| 4 |
| A．2 | B．-2 | C．
| D．-
|
∵
=2，
∴sinα-cosα=2（sinα+cosα），
解得sinα=-3cosα．
由此可得tanα=
=-3，
∴tan（α+
）=
=
=-
．
故选：D
| sinα-cosα |
| sinα+cosα |
∴sinα-cosα=2（sinα+cosα），
解得sinα=-3cosα．
由此可得tanα=
| sinα |
| cosα |
∴tan（α+
| π |
| 4 |
tanα+tan
| ||
1-tanαtan
|
| 1+(-3) |
| 1-(-3)×1 |
| 1 |
| 2 |
故选：D
练习册系列答案
相关题目
，均有
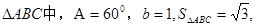，则
（ ）. 
、
； 
、
； 
、
、
．
则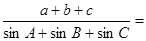
（ ）
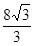
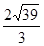
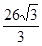
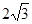
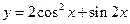的最小值是____________________ .