题目内容
4.设函数f(2x)=1og3(8x2+7),则f(1)=2.分析 由f(1)=f(2×$\frac{1}{2}$),利用函数性质能求出f(1)的值.
解答 解:∵函数f(2x)=1og3(8x2+7),
∴f(1)=f(2×$\frac{1}{2}$)=$lo{g}_{3}[8×(\frac{1}{2})^{2}+7]$=log39=2.
故答案为:2.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
14.已知i为虚数单位,则复数$\frac{3-4i}{1+i}$的虚部为( )
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{7}{2}i$ | D. | $\frac{7}{2}i$ |
15.已知复数z=$\frac{2}{i}$-i(其中i为虚数单位),则|z|=( )
| A. | 3 | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
12.下列程序输出的结果是( )
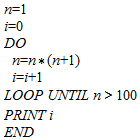
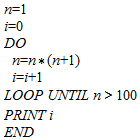
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
16.设i是虚数单位,则复数$\frac{3+4i}{1-i}$的共轭复数为( )
| A. | -$\frac{1}{2}$+$\frac{7}{2}$i | B. | -$\frac{1}{2}$-$\frac{7}{2}$i | C. | $\frac{1}{2}$-$\frac{7}{2}$i | D. | $\frac{1}{2}$+$\frac{7}{2}$i |
14.若函数f(x)=sin$\frac{x}{2}$+acos$\frac{x}{2}$的图象关于点($\frac{3π}{2}$,0)对称,则函数f(x)的最大值等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |