题目内容
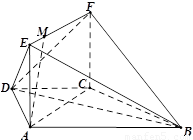
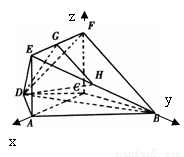
如图,在梯形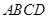 中,
中,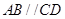 ,
,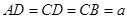 ,
,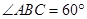 ,平面
,平面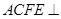 平面
平面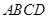 ,四边形
,四边形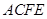 是矩形,
是矩形, ,点
,点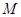 在线段EF上.
在线段EF上.
(1)求异面直线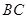 与
与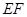 所成的角;
所成的角;
(2)求二面角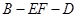 的余弦值.
的余弦值.
【答案】
(1)900 ;(2)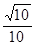 .
.
【解析】
试题分析:(1)要求异面直线所成的角,可转化为求其中一条直线与另外一直线的平行线所成的角的大小;(2)法一:利用几何法,求二面角需要先找出二面角的平面角,再在平面角所在的三角形中根据边长由余弦定理求平面角的余弦值,即二面角的余弦值;法二:利用向量法,首先建立直角坐标系,写出所需各点的坐标以及向量的坐标,再设出二面角所在两个面的法向量,利用向量垂直求出法向量的一组值,求两个法向量的夹角的余弦值,从而得二面角的余弦值.
试题解析:(1)在梯形ABCD中,∵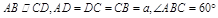 ,
,
∴四边形ABCD是等腰梯形, 且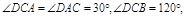
∴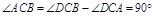 ,∴
,∴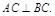
又∵平面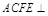 平面ABCD,交线为AC,∴
平面ABCD,交线为AC,∴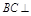 平面ACFE. ∴
平面ACFE. ∴ 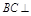 平面FE.
平面FE.
∴异面直线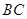 与
与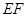 所成的角为900
7分
所成的角为900
7分
(2)方法一;(几何法)取EF中点G,EB中点H,连结DG、GH、DH,
∵容易证得DE=DF,∴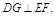
∵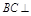 平面ACFE,∴
平面ACFE,∴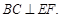 又∵
又∵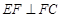 ,∴
,∴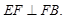
又∵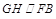 ,∴
,∴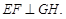
∴ 是二面角B—EF—D的平面角.
是二面角B—EF—D的平面角.
在△BDE中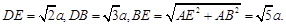
∴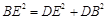 ∴
∴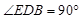 ,
,
∴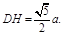 又
又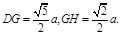 ∴在△DGH中,
∴在△DGH中,
由余弦定理得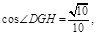 即二面角B—EF—D的平面角余弦值为
即二面角B—EF—D的平面角余弦值为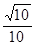 .
15分
.
15分
方法二;(向量法)以C为坐标原点,建立如图所示的直角坐标系,
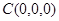 ,
,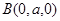 ,
,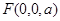 ,
,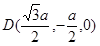 ,
,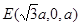
所以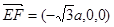 ,
,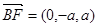 ,
,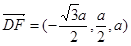
分别设平面BEF与平面DEF的法向量为
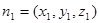 ,
,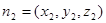
所以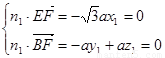 ,令
,令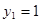 ,则
,则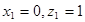
又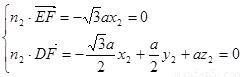 ,显然
,显然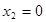 ,令
,令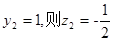
所以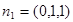 ,
,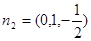 ,设二面角的平面角为
,设二面角的平面角为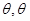 为锐角
为锐角
所以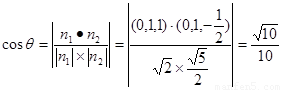 15分
15分
考点:1、异面直线所成的角;2、二面角;3、面面垂直的性质定理;4、余弦定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中,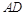 ∥BC,点
∥BC,点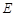 ,
, 分别在边
分别在边 ,
, 上,设
上,设 与
与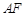 相交于点
相交于点 ,若
,若 ,
, ,
,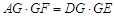 .
. 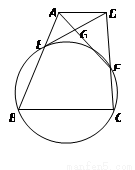
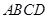 中,
中,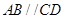 ,
,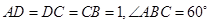 ,四边形
,四边形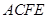 为矩
为矩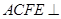 平面
平面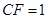 .
.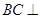 平面
平面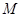 在线段
在线段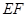 上运动,设平面
上运动,设平面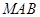 与平面
与平面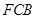 所成二面角的平面角为
所成二面角的平面角为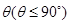 ,试求
,试求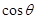

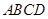 中,
中,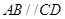 ,
,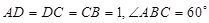 ,四边形
,四边形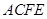 为矩形,平面
为矩形,平面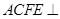 平面
平面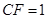 .
.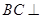 平面
平面 在线段
在线段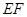 上运动,设平面
上运动,设平面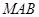 与平面
与平面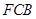 所成二面角的平面角为
所成二面角的平面角为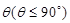 ,
,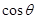 的取值范围.
的取值范围. 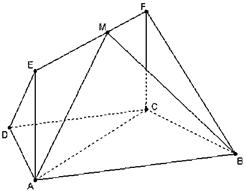
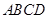 中,
中,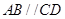 ,
,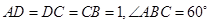 ,四边形
,四边形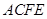 为矩形,平面
为矩形,平面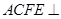 平面
平面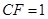 .
.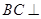 平面
平面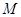 在线段
在线段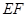 上运动,设平面
上运动,设平面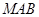 与平面
与平面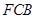 所成二面角的平面角为
所成二面角的平面角为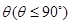 ,试求
,试求 的取值范围.
的取值范围.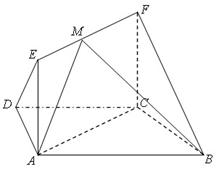
 中
中 ‖
‖ ,平面
,平面 平面
平面 是矩形,
是矩形, ,点
,点 在线段
在线段 上.
上. 平面
平面 为何值时,
为何值时, ‖平面
‖平面 ?证明你的结论;
?证明你的结论; 的大小.
的大小. 