题目内容
如图,在梯形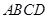 中,
中,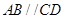 ,
,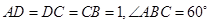 ,四边形
,四边形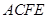 为矩
为矩
形,平面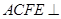 平面
平面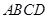 ,
,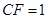 .
.
(I)求证: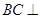 平面
平面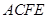 ;
;
(II)点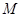 在线段
在线段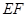 上运动,设平面
上运动,设平面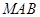 与平面
与平面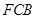 所成二面角的平面角为
所成二面角的平面角为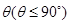 ,试求
,试求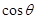
的取值范围.

【答案】
解:(I)证明:在梯形 中,
∵
中,
∵  ,
, ,
,
∠ =
= ,∴
,∴
 ∴
∴ 
∴  ∴
∴  ⊥
⊥
∵ 平面 ⊥平面
⊥平面 ,平面
,平面 ∩平面
∩平面
 ,
,
 平面
平面
∴  ⊥平面
⊥平面 …………………6分
…………………6分

(II)由(I)可建立分别以直线 为
为 的如图所示空间直角坐标系,令
的如图所示空间直角坐标系,令
 ,则
,则 ,
,
∴ 
设 为平面MAB的一个法向量,
为平面MAB的一个法向量,
由 得
得
取 ,则
,则 ,…………8分
,…………8分
∵  是平面FCB的一个法向量
是平面FCB的一个法向量
∴  ………10分
………10分
∵  ∴ 当
∴ 当 时,
时, 有最小值
有最小值 ,
,
当 时,
时, 有最大值
有最大值 。 ∴
。 ∴  …………………12分
…………………12分
解法2:(面积射影法)简解:过M做AC的垂线,垂足为H,再过M做AB的垂线,垂足为N,
连MN,则MN⊥AB,设EM= ,则MN=
,则MN= ,∴
,∴ (
( )
)
∴ 。请酌情给分。
。请酌情给分。
【解析】略

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 中,
中,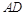 ∥BC,点
∥BC,点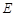 ,
, 分别在边
分别在边 ,
, 上,设
上,设 与
与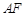 相交于点
相交于点 ,若
,若 ,
, ,
,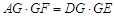 .
. 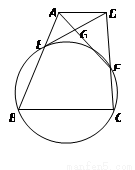
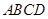 中,
中,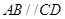 ,
,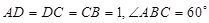 ,四边形
,四边形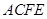 为矩形,平面
为矩形,平面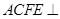 平面
平面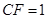 .
.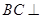 平面
平面 在线段
在线段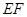 上运动,设平面
上运动,设平面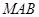 与平面
与平面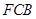 所成二面角的平面角为
所成二面角的平面角为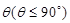 ,
,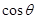 的取值范围.
的取值范围. 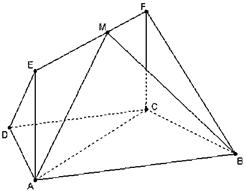
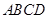 中,
中,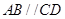 ,
,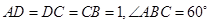 ,四边形
,四边形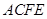 为矩形,平面
为矩形,平面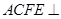 平面
平面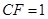 .
.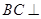 平面
平面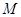 在线段
在线段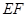 上运动,设平面
上运动,设平面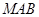 与平面
与平面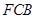 所成二面角的平面角为
所成二面角的平面角为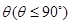 ,试求
,试求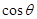 的取值范围.
的取值范围.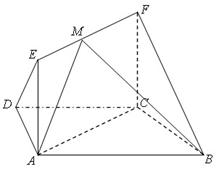
 中
中 ‖
‖ ,平面
,平面 平面
平面 是矩形,
是矩形, ,点
,点 在线段
在线段 上.
上.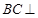 平面
平面 为何值时,
为何值时, ‖平面
‖平面 ?证明你的结论;
?证明你的结论; 的大小.
的大小. 