题目内容
已知函数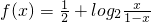 .
.
(Ⅰ)求证:f(x)的图象关于点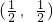 成中心对称;
成中心对称;
(Ⅱ)若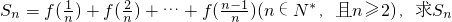 ;
;
(Ⅲ)已知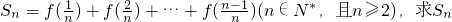 ,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围.
,数列{an}的前n项和为Tn.若Tn<λ(Sn+1+1)对一切n∈N*都成立,求λ的取值范围.
证明:(Ⅰ)在函数f(x)图象上任取一点M(x,y),M关于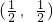 的对称点为N(x1,y1),
的对称点为N(x1,y1),
∴ ,∴
,∴ ①.
①.
∵f(x)= ,即
,即 ②.
②.
将①代入②得, =
= ,
,
∴ ,∴N(x1,y1)也在f(x)图象上,∴f(x)图象关于点
,∴N(x1,y1)也在f(x)图象上,∴f(x)图象关于点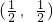 成中心对称.
成中心对称.
(直接证f(x)+f(1-x)=1得f(x)图象关于点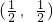 成中心对称,也可给分)(5分)
成中心对称,也可给分)(5分)
(Ⅱ)由(Ⅰ)可知f(x)+f(1-x)=1,
又∵n≥2时,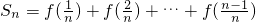 ③,
③, ④
④
③+④得2Sn=n-1,∴ .(9分)
.(9分)
(Ⅲ)由(Ⅱ)可知,当n≥2时, =
= ,
,
∴当n≥2时, =
= ;
;
∵当n=1时, 也适合上式,∴
也适合上式,∴ .
.
由Tn<λ(Sn+1+1)得, ,∴
,∴ ,即
,即 .
.
令 ,则
,则 =
= ,
,
又∵n∈N*,∴ ,
,
∴当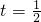 时,即n=2时,
时,即n=2时, 最大,它的最大值是
最大,它的最大值是 ,∴
,∴ .(14分)
.(14分)
分析:(I)证明函数的图象关于点M成中心对称,只需在图象上任取一点A,求出其关于中心的对称点A′的坐标,代入函数解析式也成立,即可证明成中心对称.利用以下结论:若f(x)+f(1-x)=1,则f(x)图象关于点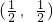 成中心对称也可证明.
成中心对称也可证明.
(II)利用(I)的结论可知f(x)+f(1-x)=1,因此运用倒序相加法的思想方法很容易解答本题.
(III)由(II)知 ,因此求得an,利用裂项相消法可以求得{an}的前n项和为Tn,于是由Tn<λ(Sn+1+1)得到 λ与n的关系式进一步利用函数与方程的思想转化为求函数的最值问题,可解得λ 的取值范围.
,因此求得an,利用裂项相消法可以求得{an}的前n项和为Tn,于是由Tn<λ(Sn+1+1)得到 λ与n的关系式进一步利用函数与方程的思想转化为求函数的最值问题,可解得λ 的取值范围.
点评:本题考查了数列与函数、函数的图象、不等式等综合内容,函数图象成中心对称的有关知识,考查相关方法,考查了数列中常用的思想方法,如倒序相加法,裂项相消法求数列前n项的和,利用函数与方程的思想,转化与化归思想解答热点问题--有关恒成立问题.
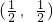 的对称点为N(x1,y1),
的对称点为N(x1,y1),∴
 ,∴
,∴ ①.
①.∵f(x)=
 ,即
,即 ②.
②.将①代入②得,
 =
= ,
,∴
 ,∴N(x1,y1)也在f(x)图象上,∴f(x)图象关于点
,∴N(x1,y1)也在f(x)图象上,∴f(x)图象关于点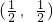 成中心对称.
成中心对称.(直接证f(x)+f(1-x)=1得f(x)图象关于点
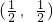 成中心对称,也可给分)(5分)
成中心对称,也可给分)(5分)(Ⅱ)由(Ⅰ)可知f(x)+f(1-x)=1,
又∵n≥2时,
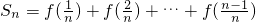 ③,
③, ④
④③+④得2Sn=n-1,∴
 .(9分)
.(9分)(Ⅲ)由(Ⅱ)可知,当n≥2时,
 =
= ,
,∴当n≥2时,
 =
= ;
;∵当n=1时,
 也适合上式,∴
也适合上式,∴ .
.由Tn<λ(Sn+1+1)得,
 ,∴
,∴ ,即
,即 .
.令
 ,则
,则 =
= ,
,又∵n∈N*,∴
 ,
,∴当
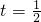 时,即n=2时,
时,即n=2时, 最大,它的最大值是
最大,它的最大值是 ,∴
,∴ .(14分)
.(14分)分析:(I)证明函数的图象关于点M成中心对称,只需在图象上任取一点A,求出其关于中心的对称点A′的坐标,代入函数解析式也成立,即可证明成中心对称.利用以下结论:若f(x)+f(1-x)=1,则f(x)图象关于点
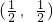 成中心对称也可证明.
成中心对称也可证明.(II)利用(I)的结论可知f(x)+f(1-x)=1,因此运用倒序相加法的思想方法很容易解答本题.
(III)由(II)知
 ,因此求得an,利用裂项相消法可以求得{an}的前n项和为Tn,于是由Tn<λ(Sn+1+1)得到 λ与n的关系式进一步利用函数与方程的思想转化为求函数的最值问题,可解得λ 的取值范围.
,因此求得an,利用裂项相消法可以求得{an}的前n项和为Tn,于是由Tn<λ(Sn+1+1)得到 λ与n的关系式进一步利用函数与方程的思想转化为求函数的最值问题,可解得λ 的取值范围.点评:本题考查了数列与函数、函数的图象、不等式等综合内容,函数图象成中心对称的有关知识,考查相关方法,考查了数列中常用的思想方法,如倒序相加法,裂项相消法求数列前n项的和,利用函数与方程的思想,转化与化归思想解答热点问题--有关恒成立问题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目





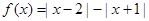 .
. ;
;
 .
. ;
; .
.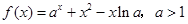 .
.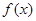 在
在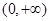 上单调递增;
上单调递增;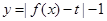 有三个零点,求
有三个零点,求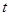 值;
值;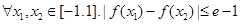 恒成立,求
恒成立,求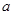 的取值范围.
的取值范围.