题目内容

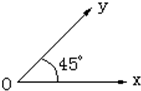
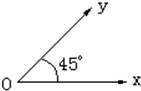在平面坐标系中，若∠xoy=α，且α∈(0，
π
2
)∪(
π
2
，π)，则称xoy为该平面上的一个斜坐标系．记
e1
、
e2
分别是x轴、y轴上的单位的向量，对于坐标平面内的点P，若
op
=x
e1
+y
e2
，那么（x，y）叫做点P的斜坐标．若已知α=
π
4
，点P的斜坐标为（
2
，1），则|
OP
|=
5
5
．
分析：由定义知P的斜坐标是（
2
，1），可得出
OP
=
e1
+
2
e2
，即|
OP
|=|
2
 e1
+
e2
|，平方得|
OP
| 2=(
2
e1
+
e2
) 2，展开运算即可．
解答：解：由题意|
OP
|=|
2
 e1
+
e2
|，
故|
OP
| 2=(
2
e1
+
e2
) 2=2
e1
2+2
2
e1
•
e2
+
e2
2=2+1+2
2
×cos45°=3+2
2
×（
2
2
）=3+2=5
即 |
OP
|=
5

故答案为：
5
点评：本题考查向量模的求法，求向量的模一般先求其平方，或者恒等变形，将其拿到根号下平方，以达到用公式求出其值的目的，解此类题时注意总结此规律，这是解本类题的通用方法，切记！本题是个新定义的题，对新定义一定要认真研究其内容及运算规律，充分理解定义再利用其规律做题．
练习册系列答案
相关题目
在直角坐标系中，若A（3，2）、B（-2，3），现沿y轴把直角坐标平面折成120°的二面角后，AB长（　　）
如图所示，将平面直角坐标系中的纵轴绕点O顺时针旋转300（坐标轴的长度单位不变）构成一个斜坐标系xOy，平面上任一点P关于斜坐标系的坐标（x，y）用如下方式定义：过P作两坐标轴的平行线分别交坐标轴Ox于点M，Oy于点N，则M在Ox轴上表示的数为x，N在Oy轴上表示的数为y．在斜坐标系中，若A，B两点的坐标分别为（1，2），（-2，3），则线段AB的长为
7
7
．
（2010•深圳二模）（坐标系与参数方程选做题）在极坐标系中，若圆C的极坐标方程为ρ2-4ρcos(θ-
π
3
)-1=0，若以极点为原点，以极轴为x轴的正半轴建立相应的平面直角坐标系xOy中，则在直角坐标系中，圆心C的直角坐标是
(1，
3
)
(1，
3
)
．
在平面坐标系中，若∠xoy=α，且α∈(0，
π
2
)∪(
π
2
，π)，则称xoy为该平面上的一个斜坐标系．记
e1
、
e2
分别是x轴、y轴上的单位的向量，对于坐标平面内的点P，若
op
=x
e1
+y
e2
，那么（x，y）叫做点P的斜坐标．若已知α=
π
4
，点P的斜坐标为（
2
，1），则|
OP
|=______．
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网