题目内容
13.已知:a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=2,求下列各式的值:(1)a2+a-2;
(2)a3+a-3;
(3)a4+a-4.
分析 根据指数幂的运算性质即可求出,
解答 解:(1)∵a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=2,
∴(a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$)2=22,
∴a+a-1=2,
∴a2+a-2=(a+a-1)2-2=22-2=2,
(2)a3+a-3=(a+a-1)(a2+a-2-1)=2×(2-1)=2,
(3)a4+a-4=(a2+a-2)2-2=22-2=2.
点评 本题考查了指数幂的运算性质,关键是掌握完全平方公式,立方差公式,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.已知函数f(x)=x2+ax+1,若存在x0,使|f(x0)|$≤\frac{1}{4}$,|f(x0+1)|≤$\frac{1}{4}$同时成立,则a的取值范围是( )
| A. | [4,6] | B. | [-$\sqrt{6}$,-2] | C. | [2,$\sqrt{6}$] | D. | [-$\sqrt{6}$,-2]∪[2,$\sqrt{6}$] |
8.函数f(x)=Asin(wx+φ)(A>0,w>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{3π}{2}$)的值是( )
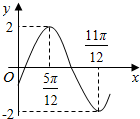

| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
19.设全集I=R,若集合M={y|y=2${\;}^{\sqrt{3+2x-{x}^{2}}}$},N={x|y=ln(x-2)},则M∩∁I(N)=( )
| A. | [2,4] | B. | [1,2] | C. | (-∞,2]∪[4,+∞) | D. | (-∞,1]∪[2,+∞) |