题目内容
将函数 的图象沿坐标轴右移,使图象的对称轴与函数
的图象沿坐标轴右移,使图象的对称轴与函数 的对称轴重合,则平移的最小单位是 .
的对称轴重合,则平移的最小单位是 .
【答案】分析:先求出函数 的对称轴,再求出函数
的对称轴,再求出函数 的图象沿坐标轴向右平移φ个单位的函数的对称轴,根据对称轴重合建立关系,给出k′和k的值求出φ的最小值.
的图象沿坐标轴向右平移φ个单位的函数的对称轴,根据对称轴重合建立关系,给出k′和k的值求出φ的最小值.
解答:解:函数 的图象的对称轴为:2x+
的图象的对称轴为:2x+ =k′π,
=k′π,
即x= ,k′∈Z;
,k′∈Z;
函数 的图象沿坐标轴向右平移φ个单位,
的图象沿坐标轴向右平移φ个单位,
得到 的图象,
的图象,
函数 的对称轴为:
的对称轴为: ,
,
即: k∈Z,
k∈Z,
由于对称轴相同, ,φ>0
,φ>0
∴当k′=1,k=0时,
所以φ的最小值为 .
.
故答案为:
点评:本题考查三角函数的图象的变换,考查三角函数的对称性,本题解题的关键是根据两个函数的对称轴相同,做出两个函数的对称轴,进行比较,在比较时注意两个系数的取值,本题是一个中档题目.
 的对称轴,再求出函数
的对称轴,再求出函数 的图象沿坐标轴向右平移φ个单位的函数的对称轴,根据对称轴重合建立关系,给出k′和k的值求出φ的最小值.
的图象沿坐标轴向右平移φ个单位的函数的对称轴,根据对称轴重合建立关系,给出k′和k的值求出φ的最小值.解答:解:函数
 的图象的对称轴为:2x+
的图象的对称轴为:2x+ =k′π,
=k′π,即x=
 ,k′∈Z;
,k′∈Z;函数
 的图象沿坐标轴向右平移φ个单位,
的图象沿坐标轴向右平移φ个单位,得到
 的图象,
的图象,函数
 的对称轴为:
的对称轴为: ,
,即:
 k∈Z,
k∈Z,由于对称轴相同,
 ,φ>0
,φ>0∴当k′=1,k=0时,
所以φ的最小值为
 .
.故答案为:

点评:本题考查三角函数的图象的变换,考查三角函数的对称性,本题解题的关键是根据两个函数的对称轴相同,做出两个函数的对称轴,进行比较,在比较时注意两个系数的取值,本题是一个中档题目.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
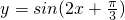 的图象沿坐标轴右移,使图象的对称轴与函数
的图象沿坐标轴右移,使图象的对称轴与函数 的对称轴重合,则平移的最小单位是________.
的对称轴重合,则平移的最小单位是________. 的图象沿坐标轴向右平移φ个单位(φ>0),使平移后图象的对称轴与函数
的图象沿坐标轴向右平移φ个单位(φ>0),使平移后图象的对称轴与函数 的图象的对称轴重合,则φ的最小值是________.
的图象的对称轴重合,则φ的最小值是________. 的图象沿坐标轴右移,使图象的对称轴与函数
的图象沿坐标轴右移,使图象的对称轴与函数 的对称轴重合,则平移的最小单位是 .
的对称轴重合,则平移的最小单位是 .