题目内容
已知|a|<1,|b|<1,求证:|
|<1.
证明:假设||≥1,那么|a+b|≥|1+ab|.则(a+b)2≥(1+ab)2
|a|≤1且|b|≥1或|a|≥1且|b|≤1,均与已知矛盾,故|
|<1.
练习册系列答案
相关题目
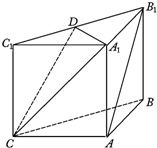如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，点D是棱B1C1的中点．
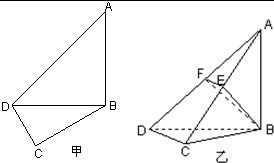在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．已知已知a+lga=10，b+10b=10，则a+b=（ ）
| A、5 | B、10 | C、15 | D、20 |
已知a，b，c∈R，那么下列命题中正确的是（ ）
| A、若a＞b，则ac2＞bc2 | ||||
B、若
| ||||
C、若a3＞b3且ab＜0，则
| ||||
D、若a2＞b2且ab＞0，则
|