题目内容
9.已知直三棱柱ABC-A1B1C1中,∠BAC=90°,侧面BCC1B1的面积为4,则直三棱柱ABC-A1B1C1外接球表面积的最小值为( )| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
分析 设BC=2x,BB1=2y,则4xy=2,利用直三棱柱ABC-A1B1C1中,∠BAC=90°,可得直三棱柱ABC-A1B1C1外接球的半径为$\sqrt{{x}^{2}+{y}^{2}}$≥$\sqrt{2xy}$=$\sqrt{2}$,即可求出三棱柱ABC-A1B1C1外接球表面积的最小值.
解答 解:设BC=2x,BB1=2y,则4xy=4,
∵直三棱柱ABC-A1B1C1中,∠BAC=90°,
∴直三棱柱ABC-A1B1C1外接球的半径为$\sqrt{{x}^{2}+{y}^{2}}$≥$\sqrt{2xy}$=$\sqrt{2}$,
∴直三棱柱ABC-A1B1C1外接球表面积的最小值为4π×2=8π.
故选:B.
点评 本题考查三棱柱ABC-A1B确定1C1外接球表面积的最小值,考查基本不等式的运用,确定直三棱柱ABC-A1B1C1外接球的半径的最小值是关键.

练习册系列答案
相关题目
4.已知角α是第二象限角,直线2x+(tanα)y+1=0的斜率为$\frac{8}{3}$,则cosα等于( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
1.某程序框图如图所示,则该程序运行后输出的值是( )


| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
19.设函数f(x)=2lnx-$\frac{3}{x}$-m,若关于x的方程f(f(x))=x恰有两个不相等的实数根,则m的取值范围是( )
| A. | (2ln3-4,+∞) | B. | (-∞,2ln3-4) | C. | (-4,+∞) | D. | (-∞,-4) |
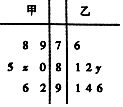 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.