题目内容
已知函数 .
.
(1)设 是函数
是函数 的极值点,求
的极值点,求 的值并讨论
的值并讨论 的单调性;
的单调性;
(2)当 时,证明:
时,证明: >
> .
.
(1)函数 在
在 上单调递减,在
上单调递减,在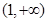 上单调递增.
上单调递增.
(2)见解析.
解析试题分析:(1)根据 是
是 的极值点得
的极值点得 ,可得导函数值为0,即
,可得导函数值为0,即 ,求得
,求得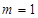 .进一步讨论导函数为正、负的区间,即得解;
.进一步讨论导函数为正、负的区间,即得解;
(2)可以有两种思路,一种是注意到当 ,
, 时,
时,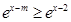 ,
,
转化成证明当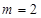 时,
时, >
> .
.
研究函数当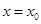 时,
时,  取得最小值且
取得最小值且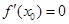 .
.
证得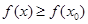 ,
,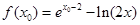 =
=
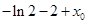 =
=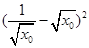

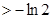 .
.
得证.
第二种思路是:当 ,
, 时,
时,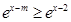 ,根据
,根据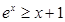 ,转化成
,转化成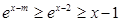 .
.
构造函数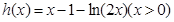
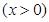 ,研究得到函数
,研究得到函数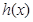 在
在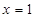 时取唯一的极小值即最小值为
时取唯一的极小值即最小值为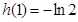 .达到证明目的.
.达到证明目的.
试题解析:(1)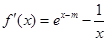 ,由
,由 是
是 的极值点得
的极值点得 ,
,
即 ,所以
,所以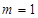 . 2分
. 2分
于是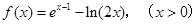 ,
,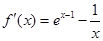 ,
,
由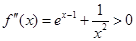 知
知 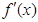 在
在 上单调递增,且
上单调递增,且 ,
,
所以 是
是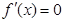 的唯一零点. 4分
的唯一零点. 4分
因此,当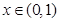 时,
时, ;当
;当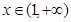 时,
时,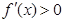 ,所以,函数
,所以,函数 在
在 上单调递减,在
上单调递减,在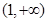 上单调递增. 6分
上单调递增. 6分
(2)解法一:当 ,
, 时,
时,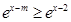 ,
,
故只需证明当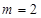 时,
时, >
> . 8分
. 8分
当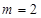 时,函数
时,函数 在
在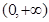 上单调递增,
上单调递增,
又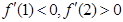 ,
,
故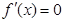 在
在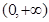 上有唯一实根
上有唯一实根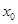 ,且
,且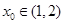 . 10分
. 10分
当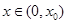 时,
时, ;当
;当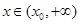 时,
时,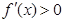 ,
,
从而当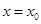

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
 ,函数
,函数 .
.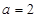 ,求函数
,求函数 在区间
在区间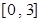 上的最大值;
上的最大值;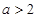 ,写出函数
,写出函数 ,使得关于
,使得关于 的方程
的方程 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数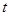 的取值范围.
的取值范围.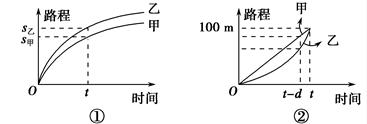
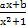 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0. x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.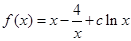 ,其中
,其中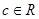 ,
,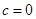 时,求曲线
时,求曲线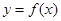 在点
在点 处的切线方程;
处的切线方程;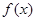 的单调性;
的单调性; 和
和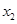 ,记过点
,记过点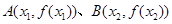 的直线的斜率为
的直线的斜率为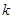 ,问是否存在
,问是否存在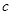 ,使得
,使得 ?若存在,求出
?若存在,求出