题目内容
已知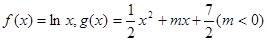 ,直线
,直线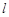 与函数
与函数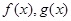 的图像都相切,且与函数
的图像都相切,且与函数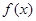 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(1)求直线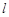 的方程及
的方程及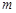 的值;
的值;
(2)若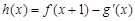 (其中
(其中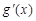 是
是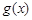 的导函数),求函数
的导函数),求函数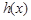 的最大值;
的最大值;
(3)当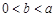 时,求证:
时,求证: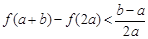 .
.
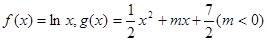 ,直线
,直线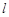 与函数
与函数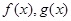 的图像都相切,且与函数
的图像都相切,且与函数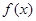 的图像的切点的横坐标为1.
的图像的切点的横坐标为1. (1)求直线
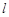 的方程及
的方程及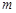 的值;
的值;(2)若
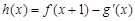 (其中
(其中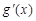 是
是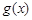 的导函数),求函数
的导函数),求函数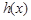 的最大值;
的最大值;(3)当
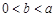 时,求证:
时,求证: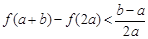 .
.(1) ,m=-2
,m=-2
(2)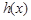 取得最大值
取得最大值
(3)由(Ⅱ)知:当 时,
时, ,即
,即 ,结合单调性来证明。
,结合单调性来证明。
 ,m=-2
,m=-2(2)
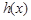 取得最大值
取得最大值
(3)由(Ⅱ)知:当
 时,
时, ,即
,即 ,结合单调性来证明。
,结合单调性来证明。试题分析:解:(Ⅰ)依题意知:直线
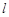 是函数
是函数 在点
在点 处的切线,故其斜率
处的切线,故其斜率 ,所以直线
,所以直线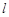 的方程为
的方程为 .又因为直线
.又因为直线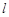 与
与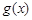 的图像相切,所以由
的图像相切,所以由 ,
,得
 (
( 不合题意,舍去); . 4分
不合题意,舍去); . 4分(Ⅱ)因为
 (
( ),所以
),所以 .当
.当 时,
时, ;当
;当 时,
时, .
.因此,
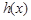 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减. 因此,当
 时,
时,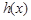 取得最大值
取得最大值 ; . 8分
; . 8分(Ⅲ)当
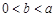 时,
时, .由(Ⅱ)知:当
.由(Ⅱ)知:当 时,
时, ,即
,即 .因此,有
.因此,有 . . 12分
. . 12分点评:主要是考查了函数的单调性以及不等式的运用,属于基础题。

练习册系列答案
相关题目
 ,
, ,则函数
,则函数 的值域为( )
的值域为( )



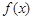 的定义域为D,如果
的定义域为D,如果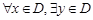 ,使
,使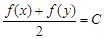 (C为常数
(C为常数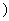 成立,则称函数
成立,则称函数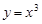 ;②
;②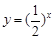 ;③
;③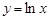 ;④
;④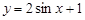 ,则满足在其定义域上均值为1的函数的个数是( )
,则满足在其定义域上均值为1的函数的个数是( )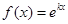 (
(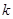 是不为零的实数,
是不为零的实数,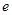 为自然对数的底数).
为自然对数的底数).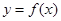 与
与 有公共点,且在它们的某一公共点处有共同的切线,求k的值;
有公共点,且在它们的某一公共点处有共同的切线,求k的值;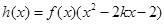 在区间
在区间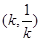 内单调递减,求此时k的取值范围.
内单调递减,求此时k的取值范围.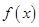 是定义在区间
是定义在区间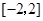 上的偶函数,当
上的偶函数,当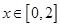 时,
时,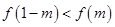 成立,求实数
成立,求实数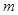 的取值范围.( )
的取值范围.( )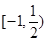
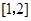
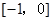
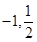 )
)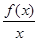 在I上是减函数,则称y=f(x)在I 上是“弱增函数”.已知函数h(x)=x2-(b-1)x+b在(0,1]上是“弱增函数”,则实数b的值为 .
在I上是减函数,则称y=f(x)在I 上是“弱增函数”.已知函数h(x)=x2-(b-1)x+b在(0,1]上是“弱增函数”,则实数b的值为 . 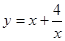
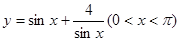
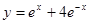
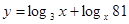
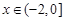 时,f(x)= -x(2+x),当
时,f(x)= -x(2+x),当 时,f(x)=(x-2)(a-x)(
时,f(x)=(x-2)(a-x)(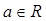 ).关于偶函数f(x)的图象G和直线
).关于偶函数f(x)的图象G和直线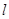 :y=m(
:y=m(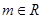 )的3个命题如下:
)的3个命题如下: 时,直线
时,直线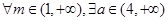 ,使得直线
,使得直线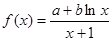 在点
在点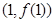 处的切线方程为
处的切线方程为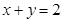 .
.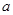 ,
,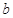 的值;
的值;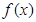 定义域内的任一个实数
定义域内的任一个实数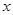 ,
,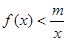 恒成立,求实数
恒成立,求实数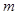 的取值范围.
的取值范围.