题目内容
求函数f(x)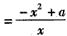 (a>0)的单调区间.
(a>0)的单调区间.
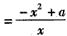 (a>0)的单调区间.
(a>0)的单调区间.解: ,
,
∵ 的单调递减区间是(-∞,0)和(0,+∞),y=-x在R上单调递减,
的单调递减区间是(-∞,0)和(0,+∞),y=-x在R上单调递减,
∴f(x)= (a>0)的单调递减区间是(-∞,0)和(0,+∞)。
(a>0)的单调递减区间是(-∞,0)和(0,+∞)。
 ,
,∵
 的单调递减区间是(-∞,0)和(0,+∞),y=-x在R上单调递减,
的单调递减区间是(-∞,0)和(0,+∞),y=-x在R上单调递减,∴f(x)=
 (a>0)的单调递减区间是(-∞,0)和(0,+∞)。
(a>0)的单调递减区间是(-∞,0)和(0,+∞)。 
练习册系列答案
相关题目
题目内容
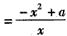 (a>0)的单调区间.
(a>0)的单调区间. ,
, 的单调递减区间是(-∞,0)和(0,+∞),y=-x在R上单调递减,
的单调递减区间是(-∞,0)和(0,+∞),y=-x在R上单调递减, (a>0)的单调递减区间是(-∞,0)和(0,+∞)。
(a>0)的单调递减区间是(-∞,0)和(0,+∞)。 