题目内容
1.已知函数f(x)=$\sqrt{3}$sinx+cosx.(1)求f(x)的最大值;
(2)设g(x)=f(x)cosx,x∈[0,$\frac{π}{2}$],求g(x)的值域.
分析 (1)利用三角恒等变换,化简函数f(x)的解析式,再利用正弦函数的值域求得它的最大值.
(2)利用三角恒等变换,化简函数g(x)的解析式,再利用正弦函数的定义域和值域求得它的值域.
解答 解:(1)∵函数f(x)=$\sqrt{3}$sinx+cosx=2sin(x+$\frac{π}{6}$),故函数f(x)=$\sqrt{3}$sinx+cosx的最大值为2.
(2)∵x∈[0,$\frac{π}{2}$],∴x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],∴g(x)=f(x)cosx=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1+cos2x}{2}$=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$∈[1,$\frac{3}{2}$],
即函数g(x)的值域为[1,$\frac{3}{2}$].
点评 本题主要考查三角恒等变换,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
12.设a=$\sqrt{6}$+$\sqrt{7}$,b=$\sqrt{5}$+$\sqrt{8}$,c=5,则a、b、c的大小关系为( )
| A. | c<b<a | B. | b<c<a | C. | c<a<b | D. | a<b<c |
9.若集合A={-2,-1,0,1,2},B={x||x|≤1},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1} | C. | {x|-1≤x≤1} | D. | {x|0≤x≤1} |
6.函数g(x)=-x2+2lnx的图象大致是( )
| A. |  | B. | 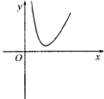 | C. | 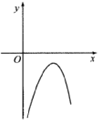 | D. | 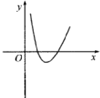 |