题目内容
(2013•徐州模拟)已知椭圆E:
+
=1(a>b>0)的离心率为
,右焦点为F,且椭圆E上的点到点F距离的最小值为2.
(1)求椭圆E的方程;
(2)设椭圆E的左、右顶点分别为A,B,过点A的直线l与椭圆E及直线x=8分别相交于点M,N.
(ⅰ)当过A,F,N三点的圆半径最小时,求这个圆的方程;
(ⅱ)若cos∠AMB=-
,求△ABM的面积.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆E的方程;
(2)设椭圆E的左、右顶点分别为A,B,过点A的直线l与椭圆E及直线x=8分别相交于点M,N.
(ⅰ)当过A,F,N三点的圆半径最小时,求这个圆的方程;
(ⅱ)若cos∠AMB=-
| ||
| 65 |
分析:(1)由离心率为
,椭圆E上的点到点F距离的最小值为2,即a-c=2联立方程组求a,c的值,然后利用b2=a2-c2求出b2,则椭圆方程可求;
(2)(ⅰ)设出圆的一般方程,设N(8,t),把三点A(-4,0),F(2,0),N(8,t)代入圆的方程整理成标准式后利用基本不等式求出半径的最小值,同时求得半径最小时的圆的方程;
(ⅱ)设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M点的坐标,由cos∠AMB=-
,借助于向量数量积求出直线的斜率,进一步得到M点的纵坐标,则△ABM的面积可求.
| 1 |
| 2 |
(2)(ⅰ)设出圆的一般方程,设N(8,t),把三点A(-4,0),F(2,0),N(8,t)代入圆的方程整理成标准式后利用基本不等式求出半径的最小值,同时求得半径最小时的圆的方程;
(ⅱ)设出直线l的方程,和椭圆方程联立后利用根与系数关系求出M点的坐标,由cos∠AMB=-
| ||
| 65 |
解答:解:(1)由已知,
=
,且a-c=2,所以a=4,c=2,所以b2=a2-c2=12,
所以椭圆E的方程为
+
=1.
(2)(ⅰ)由(1),A(-4,0),F(2,0),设N(8,t).
设圆的方程为x2+y2+dx+ey+f=0,将点A,F,N的坐标代入,得
,解得
.
所以圆的方程为x2+y2+2x-(t+
)y-8=0,
即(x+1)2+[y-
(t+
)]2=9+
(t+
)2,
因为(t+
)2≥(2
)2,当且仅当t+
=±12
时,圆的半径最小,
故所求圆的方程为x2+y2+2x±12
y-8=0.
(ⅱ)由对称性不妨设直线l的方程为y=k(x+4)(k>0).
由
,得(3+4k2)x2+32k2x+64k2-48=0
由-4+xM=-
,得xM=
,所以M(
,
),
所以
=(
,
),
=(
,
),
所以cos∠AMB=
=
=-
,
化简,得16k4-40k2-9=0,
解得k2=
,或k2=
,即k=
,或k=
,
此时总有yM=3,所以△ABM的面积为
×8×3=12.
| c |
| a |
| 1 |
| 2 |
所以椭圆E的方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)(ⅰ)由(1),A(-4,0),F(2,0),设N(8,t).
设圆的方程为x2+y2+dx+ey+f=0,将点A,F,N的坐标代入,得
|
|
所以圆的方程为x2+y2+2x-(t+
| 72 |
| t |
即(x+1)2+[y-
| 1 |
| 2 |
| 72 |
| t |
| 1 |
| 4 |
| 72 |
| t |
因为(t+
| 72 |
| t |
| 72 |
| 72 |
| t |
| 2 |
故所求圆的方程为x2+y2+2x±12
| 2 |
(ⅱ)由对称性不妨设直线l的方程为y=k(x+4)(k>0).
由
|
由-4+xM=-
| 32k2 |
| 3+4k2 |
| 12-16k2 |
| 3+4k2 |
| 12-16k2 |
| 3+4k2 |
| 24k |
| 3+4k2 |
所以
| MA |
| -24 |
| 3+4k2 |
| -24k |
| 3+4k2 |
| MB |
| 32k2 |
| 3+4k2 |
| -24k |
| 3+4k2 |
所以cos∠AMB=
| ||||
|
|
| -8×24k | ||||
24
|
| ||
| 65 |
化简,得16k4-40k2-9=0,
解得k2=
| 1 |
| 4 |
| 9 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
此时总有yM=3,所以△ABM的面积为
| 1 |
| 2 |
点评:本题考查了圆与椭圆的标准方程,考查了直线与圆锥曲线的关系,直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题、面积问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题.

练习册系列答案
相关题目
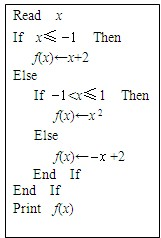 (2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是
(2013•徐州模拟)已知某算法的伪代码如图,根据伪代码,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是