题目内容
已知点F(-c,0)(c>0)是双曲线
-
=1的左焦点,离心率为e,过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P,且点P在抛物线y2=4cx上,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质、相似三角形的性质即可得出.
解答:
解:如图,设抛物线y2=4cx的准线为l,作PQ⊥l于Q,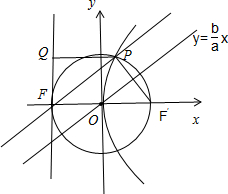
设双曲线的右焦点为F′,P(x,y).
由题意可知FF′为圆x2+y2=c2的直径,
∴PF′⊥PF,且tan∠PFF′=
,|FF′|=2c,
满足
,
将①代入②得x2+4cx-c2=0,
则x=-2c±
c,
即x=(
-2)c,(负值舍去)
代入③,即y=
,再将y代入①得,
=
=e2-1
即e2=1+
=
.
故选:D.

设双曲线的右焦点为F′,P(x,y).
由题意可知FF′为圆x2+y2=c2的直径,
∴PF′⊥PF,且tan∠PFF′=
| b |
| a |
满足
|
将①代入②得x2+4cx-c2=0,
则x=-2c±
| 5 |
即x=(
| 5 |
代入③,即y=
bc(
| ||
| a |
| b2 |
| a2 |
4(
| ||
(
|
即e2=1+
4
| ||
6-2
|
| ||
| 2 |
故选:D.
点评:本题考查双曲线的性质,掌握抛物线的性质、双曲线的渐近线、直线平行的性质、圆的性质是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
如果函数f(x)=sin(ωx+
)(ω>0)的最小正周期为π,则ω的值为( )
| π |
| 6 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
直线l过双曲线的右焦点,斜率为
,若l与双曲线的两个交点分别在其两支上,则双曲线的离心率的取值范围为( )
| 2 |
A、[
| ||
| B、(2,+∞) | ||
C、[
| ||
D、(
|
向量
=(3,-4),向量|
|=2,若
•
=-5,那么向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若对于任意的x∈(-∞,-1],不等式(3m-1)2x<1恒成立,则正实数m的取值范围是( )
| A、(-∞,1) |
| B、(-∞,1] |
| C、(0,1] |
| D、(0,1) |
已知函数 f(x)=
.若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是( )
| 4x+k•2x+1 |
| 4x+2x+1 |
| A、0<k≤3 | ||
| B、1≤k≤4 | ||
C、-
| ||
D、-
|