题目内容
若正数a,b满足a+b=1,则
+
的最大值是 .
| a |
| a+1 |
| b |
| b+1 |
分析:由于正数a,b满足a+b=1,可化为
+
=
=2-
,再利用ab≤(
)2即可得出.
| a |
| a+1 |
| b |
| b+1 |
| a(b+1)+b(a+1) |
| (a+1)(b+1) |
| 3 |
| ab+2 |
| a+b |
| 2 |
解答:解:∵正数a,b满足a+b=1,
∴
+
=
=
=
=
=2-
≤2-
=2-
=
.当且仅当a=b=
时取等号.
∴
+
的最大值是
.
故答案为:
.
∴
| a |
| a+1 |
| b |
| b+1 |
| a(b+1)+b(a+1) |
| (a+1)(b+1) |
| 2ab+a+b |
| ab+a+b+1 |
=
| 2ab+1 |
| ab+2 |
| 2(ab+2)-3 |
| ab+2 |
| 3 |
| ab+2 |
| 3 | ||
(
|
| 3 | ||
|
| 2 |
| 3 |
| 1 |
| 2 |
∴
| a |
| a+1 |
| b |
| b+1 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
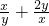 ≥2
≥2 
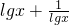 ≥2
≥2  ≥4
≥4