题目内容
下列命题
①x,y>0时,
+
≥2
②函数f(x)=
的最小值为2
③lgx+
≥2
④若正数a、b满足a+b=1,则(a+
)(b+
)≥4
其中一定成立的是
①x,y>0时,
| x |
| y |
| 2y |
| x |
②函数f(x)=
| x2+2 | ||
|
③lgx+
| 1 |
| lgx |
④若正数a、b满足a+b=1,则(a+
| 1 |
| a |
| 1 |
| b |
其中一定成立的是
①②④
①②④
(只需填写序号)分析:本题考查基本不等式的应用,根据使用条件:“一正,二定,三相等”,即可判断出每个命题是否成立.
解答:解:①∵x,y>0,∴由基本不等式得
+
≥2
=2
>2(当且仅当
=
时取“=”号).由此可知①一定成立.
②∵f(x)=
=
+
≥2,当且仅当
=
,即x=0时取“=”号,因此函数f(x)的最小值为2.
③当lgx<0时,lgx+
<0,故③不成立.
④∵a>0,b>0,∴(a+
)(b+
)≥2
×2
=4,当且仅当
,即a=b=1时取“=”号.
又∵a+b=1,∴“=”号不成立.∴(a+
)(b+
)>4,故④一定成立.
故一定成立的是①②④.
| x |
| y |
| 2y |
| x |
|
| 2 |
| x |
| y |
| 2 |
②∵f(x)=
| x2+2 | ||
|
| x2+1 |
| 1 | ||
|
| x2+1 |
| 1 | ||
|
③当lgx<0时,lgx+
| 1 |
| lgx |
④∵a>0,b>0,∴(a+
| 1 |
| a |
| 1 |
| b |
a×
|
b×
|
|
又∵a+b=1,∴“=”号不成立.∴(a+
| 1 |
| a |
| 1 |
| b |
故一定成立的是①②④.
点评:本题主要考查基本不等式,特别要注意使用条件:一正,二定,三相等.

练习册系列答案
相关题目
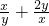 ≥2
≥2 
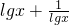 ≥2
≥2  ≥4
≥4