题目内容
（2013•南京二模）选修4-5：不等式选讲
若正数a，b满足a+b=1，求
+
的最小值．
若正数a，b满足a+b=1，求
| 1 |
| 3a+2 |
| 4 |
| 3b+2 |
分析：由题意可得 （3a+2）+（3b+2）=7，再根据
+
=
[5+
+
]，利用基本不等式求得它的最小值．
| 1 |
| 3a+2 |
| 4 |
| 3b+2 |
| 1 |
| 7 |
| 3b+2 |
| 3a+2 |
| 4(3a+2) |
| 3b+2 |
解答：解：∵正数a，b满足a+b=1，∴（3a+2）+（3b+2）=7，
∴
+
=
•（
+
）•[（3a+2）+（3b+2）]=
[5+
+
]≥
（5+2
）=
，
当且仅当
=
，即 a=
，且b=
时，等号成立，
故
+
的最小值为
．
∴
| 1 |
| 3a+2 |
| 4 |
| 3b+2 |
| 1 |
| 7 |
| 1 |
| 3a+2 |
| 4 |
| 3b+2 |
| 1 |
| 7 |
| 3b+2 |
| 3a+2 |
| 4(3a+2) |
| 3b+2 |
| 1 |
| 7 |
| 4 |
| 9 |
| 7 |
当且仅当
| 3b+2 |
| 3a+2 |
| 4(3a+2) |
| 3b+2 |
| 1 |
| 9 |
| 8 |
| 9 |
故
| 1 |
| 3a+2 |
| 4 |
| 3b+2 |
| 9 |
| 7 |
点评：本题主要考查基本不等式的应用，式子的变形是解题的关键，属于中档题．
练习册系列答案
相关题目
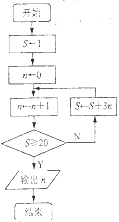（2013•南京二模）如图是一个算法流程图，其输出的n的值是