题目内容
已知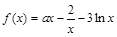 ,其中
,其中 为常数.
为常数.
(Ⅰ)当函数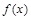 的图象在点
的图象在点 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数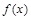 在
在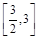 上的最小值;
上的最小值;
(Ⅱ)若函数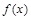 在
在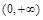 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数 的取值范围;
的取值范围;
(Ⅲ)在(Ⅰ)的条件下,过点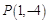 作函数
作函数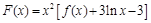 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ) .
.
解析试题分析:(Ⅰ)首先求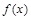 的导数,利用导数的几何意义列出方程
的导数,利用导数的几何意义列出方程 解这个方程即可得
解这个方程即可得 的值,从而得函数
的值,从而得函数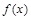 的解析式,最后利用求闭区间上函数最值的一般步骤求
的解析式,最后利用求闭区间上函数最值的一般步骤求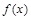 在
在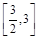 上的最小值;
上的最小值;
(Ⅱ)先求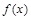 的导数:
的导数: ,根据已知
,根据已知 在
在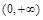 上有两不相等的实数根,将问题转化为一元二次方程
上有两不相等的实数根,将问题转化为一元二次方程 在
在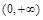 上有两不相等的实数根,最后利用根的判别式及韦达定理列不等式组解决问题;(Ⅲ)由已知
上有两不相等的实数根,最后利用根的判别式及韦达定理列不等式组解决问题;(Ⅲ)由已知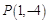 不一定是切点,需先设切点
不一定是切点,需先设切点 根据导数的几何意义,求函数在切点处的导函数值
根据导数的几何意义,求函数在切点处的导函数值 ,再分(1)切点
,再分(1)切点 不与点
不与点 重合;(2)切点
重合;(2)切点 与点
与点 重合,两种情况求曲线的切线方程.
重合,两种情况求曲线的切线方程.
试题解析:(Ⅰ) 由已知得
由已知得 解得
解得 1分
1分
故 由
由 得
得 2分
2分 随
随 的变化关系如下表:
的变化关系如下表:










↘ 
↗

练习册系列答案
相关题目
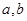 是正实数,设函数
是正实数,设函数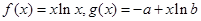 。
。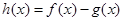 ,求
,求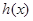 的单调区间;
的单调区间;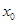 ,使
,使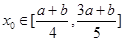 且
且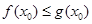 成立,求
成立,求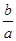 的取值范围。
的取值范围。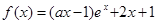 在
在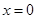 处取得极值.
处取得极值. 的值;
的值; 时,
时, .
. .
.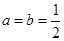 时,求函数
时,求函数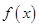 的最大值;
的最大值;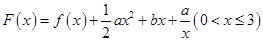 其图象上任意一点
其图象上任意一点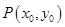 处切线的斜率
处切线的斜率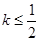 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;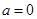 ,
, ,方程
,方程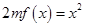 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.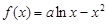 .
. 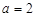 时,求函数
时,求函数 在
在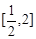 上的最大值;
上的最大值;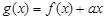 ,若
,若 在区间
在区间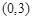 上不单调,求
上不单调,求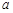 的取值范围;
的取值范围;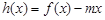 的图象与
的图象与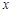 轴交于两点
轴交于两点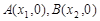 ,且
,且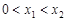 ,又
,又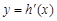 是
是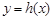 的导函数.若正常数
的导函数.若正常数 满足条件
满足条件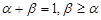 ,证明:
,证明: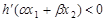 .
.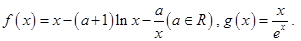
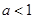 时,若存在
时,若存在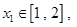 使得对任意的
使得对任意的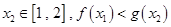 恒成立,求
恒成立,求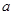 的取值范围。
的取值范围。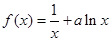 (
( ≠0,
≠0,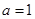 ,求函数
,求函数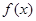 的极值和单调区间;
的极值和单调区间;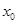 ,使得
,使得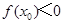 成立,求实数
成立,求实数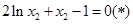
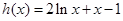 时,求函数
时,求函数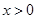 的最大值;
的最大值;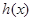 (
(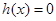 )其图象上任意一点
)其图象上任意一点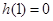 处切线的斜率
处切线的斜率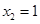 ≤
≤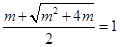 恒成立,求实数
恒成立,求实数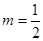 的取值范围;
的取值范围;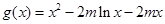 ,
,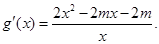 ,方程
,方程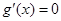 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. 。
。 时,求函数
时,求函数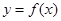 的单调区间;
的单调区间;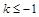 时,对所有的
时,对所有的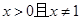 都有
都有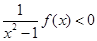 成立.
成立.