题目内容
已知f(
)的定义域为[0,3],则f(2x-1)的定义域为
| x+1 |
[1,
]
| 3 |
| 2 |
[1,
]
.| 3 |
| 2 |
分析:先由函数f(
的定义域为[0,3],求出函数f(x)的定义域,再让2x-1在f(x)的定义域内求出x的范围,从而得到函数f(2x-1)的定义域.
| x+1) |
解答:解:因为f(
的定义域为[0,3],由0≤x≤3,得1≤x+1≤4,所以1≤
≤2,
即函数f(x)的定义域为[1,2],再由1≤2x-1≤2,得1≤x≤
,
所以函数f(2x-1)的定义域为[1,
].
故答案为[1,
].
| x+1) |
| x+1 |
即函数f(x)的定义域为[1,2],再由1≤2x-1≤2,得1≤x≤
| 3 |
| 2 |
所以函数f(2x-1)的定义域为[1,
| 3 |
| 2 |
故答案为[1,
| 3 |
| 2 |
点评:本题考查了函数定义域及其求法,对于复合函数定义域求法如下:(1)给出了函数f(x)的定义域[a,b],求函数f[g(x)]的定义域,只要让a≤g(x)≤b,求解x即可;(2)给出函数f[g(x)]的定义域为[c,d],是指给出了x的范围,求出g(x)的值域,即为函数f(x)的定义域.

练习册系列答案
相关题目
 及定点F(1,0),动点M,N,G满足
及定点F(1,0),动点M,N,G满足 -
-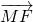 =2
=2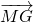 ,
,