题目内容
5．已知{an}的前n项和为${S_n}=1-5+9-13+17-21+…+{（{-1}）^{n-1}}（{4n-3}）$，则S17的值是（ ）| A． | -32 | B． | 33 | C． | 97 | D． | -97 |
分析 由已知得S17=（1-5）+（9-13）+…+（57-61）+65，由此能求出结果．
解答 解：∵Sn=1-5+9-13+17-21+…+（-1）n-1•（4n-3），
∴S17=（1-5）+（9-13）+…+（57-61）+65=8×（-4）+65=33，
故选：B．
点评 本题考查数列的前17项和的求法，是基础题，解题时要认真审题，注意总结规律．
练习册系列答案
相关题目
15．已知函数f（x）=ax-1+4的图象恒过定点P，则点P的坐标是（ ）
| A． | （1，5） | B． | （1，4） | C． | （0，4） | D． | （4，0） |
16．|$\overrightarrow{a}$|=2，向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为120°，则向量$\overrightarrow{a}$在向量$\overrightarrow{b}$方向上的投影等于（ ）
| A． | 2 | B． | 1 | ||
| C． | -1 | D． | 由向量 b 的长度确定 |
13．
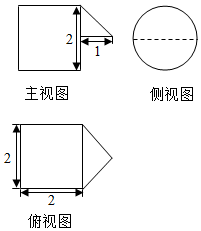某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{1}{3}+2π$ | B． | $\frac{13}{6}π$ | C． | $\frac{7π}{3}$ | D． | $\frac{5π}{2}$ |