题目内容
16.已知(5,0)是双曲线$\frac{x^2}{16}-\frac{y^2}{b^2}$=1(b>0)的一个焦点,则b=3,该双曲线的渐近线方程为y=±$\frac{3}{4}$x.分析 由题意可得c=5,即16+b2=25,解得b,进而得到双曲线的方程,即可得到渐近线方程.
解答 解:由题意可得c=5,即16+b2=25,
解得b=3,
即有双曲线的方程为$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1,
可得渐近线方程为y=±$\frac{3}{4}$x.
故答案为:3,y=±$\frac{3}{4}$x.
点评 本题考查双曲线的方程和渐近线方程的求法,注意运用双曲线的基本量的关系和渐近线方程与双曲线的方程的关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
11.双曲线x2-$\frac{y^2}{2}$=1的渐近线方程为( )
| A. | x±2y=0 | B. | 2x±y=0 | C. | $x±\sqrt{2}y=0$ | D. | $\sqrt{2}x±y=0$ |
1.已知双曲线C:$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$的焦距为$10\sqrt{5}$,点P(1,2)在双曲线C的渐近线上,则双曲线C的方程为( )
| A. | $\frac{y^2}{20}-\frac{x^2}{5}=1$ | B. | $\frac{y^2}{5}-\frac{x^2}{20}=1$ | C. | $\frac{y^2}{100}-\frac{x^2}{25}=1$ | D. | $\frac{y^2}{25}-\frac{x^2}{100}=1$ |
8.已知双曲线的左、右焦点分别是F1、F2,过F2的直线交双曲线的右支于P、Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{10}{3}$ | C. | 2 | D. | $\frac{7}{5}$ |
5.已知点F1,F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,点A是双曲线右支上一点,∠AF2F1=$\frac{2π}{3}$,且($\overrightarrow{{F}_{2}{F}_{1}}$+$\overrightarrow{{F}_{2}A}$)•$\overrightarrow{{F}_{1}A}$=0,则此双曲线的离心率为( )
| A. | $\frac{1+\sqrt{5}}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1+\sqrt{2}}{2}$ |
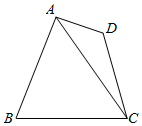 如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.
如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.